Question

Two charge particle P & Q having same charge $1{\rm{\mu C}}$ and mass ${\rm{4\mu kg}}$ are initially kept at the distance of $1\;{\rm{mm}}$. Charge P is fixed, then the velocity of charge particle Q when the separation between them becomes ${\rm{9mm}}$.
A) $3 \times {10^8}\,{\rm{m/s}}$
B) $2 \times {10^8}\,{\rm{m/s}}$
C) $5 \times {10^8}\,{\rm{m/s}}$
D) $7 \times {10^8}\,{\rm{m/s}}$

Answer 1

When two charged particles are kept at a distance say d, then there will be potential energy between the charges. This potential energy is due to the field created due to these charges.

Complete step by step answer:
Given:
The magnitude of charges on P and Q is $1{\rm{\mu C}}$.
The mass of charges on P and Q is ${\rm{4\mu kg}}$.
The distance between the charges is $1\;{\rm{mm}}$.
The following diagram represents the given scenario:

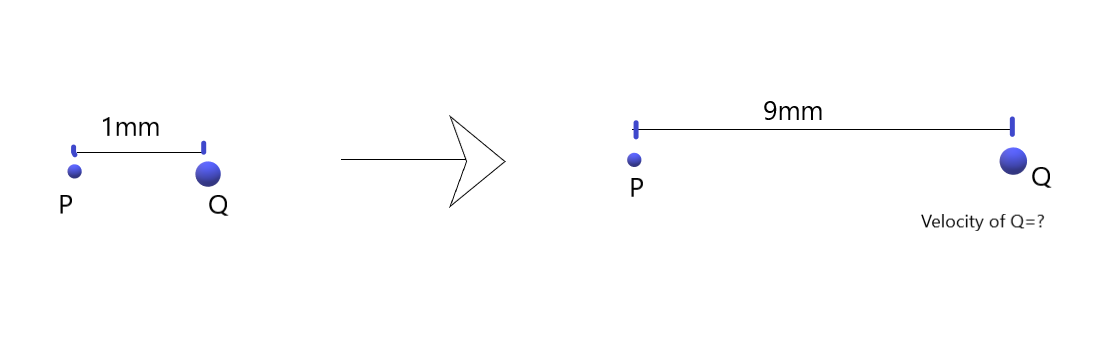
When the separation between the charged particle is increased, then there will be a considerable amount of work done in doing so that will decrease the potential energy.
We know that the formula for loss in potential energy is,
$PE = kQq\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right]$
Here, $k$ is constant and is $9 \times {10^9}\;{\rm{N }}{{\rm{m}}^2}/{\rm{C}}$, $Q$, $q$ are the two charges and ${r_1}$, ${r_2}$ are the initial and final separation between the charges.
This energy will increase the kinetic energy of the charged particle.
The formula for kinetic energy can be given as,
$KE = \dfrac{1}{2}m{v^2}$
Here, $m$ is mass and $v$ is velocity.
We know that the energy is conserved, only its form is changed, so the loss in potential energy is the gain in kinetic energy.
$\Rightarrow PE = KE$
$\Rightarrow kQq\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right] = \dfrac{1}{2}m{v^2}$
$\Rightarrow v = \sqrt {\dfrac{{2kQq}}{m}\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right]}$
We can now substitute the known values in the above equation.
$\Rightarrow v = \sqrt {\dfrac{{2 \times 9 \times {{10}^9} \times {{10}^{ - 6}} \times {{10}^{ - 6}}}}{{4 \times {{10}^{ - 6}}}}\left[ {\dfrac{1}{{{{10}^{ - 3}}}} - \dfrac{1}{{9 \times {{10}^{ - 3}}}}} \right]}$
$\Rightarrow v= 2 \times {10^3}\;{\rm{m/s}}$

$\therefore$ The velocity of charge particle Q when the separation between them becomes ${\rm{9mm}}$ is $2 \times {10^3}\;{\rm{m/s}}$, so from the given options, option B is correct.

Note:
Make sure to remember that there will be a loss in potential energy. This loss in potential will be converted to gain in kinetic energy. The law of conservation of energy will be applied here. Also, convert the units to standard units, as the units in the question are not in standard form.