Question
Question: Two cells of internal resistances \({{r}_{1}}\) and \({{r}_{2}}\) and of same emf are connected in s...
Two cells of internal resistances r1 and r2 and of same emf are connected in series, across a resistor of resistance R. If the terminal potential difference across the cells of internal resistance r1 is zero, then the value of R is?
A.R=2(r1+r2)
B.R=r2−r1
C.R=r1−r2
D.R=2(r1−r2)
Solution
Hint: Making a circuit diagram of the problem will help in understanding the problem better. The Ohm’s law, given by V=IR will be required to solve this problem. The effective current in the circuit given by the ratio of the effective potential in the circuit and the effective resistance in the circuit, that is Ieff=ReffEeff. The terminal potential of the cell E1 is given by, Vterminal=E1−Ieffr1.
Step by step solution:
Let’s start by making a circuit diagram of the problem.
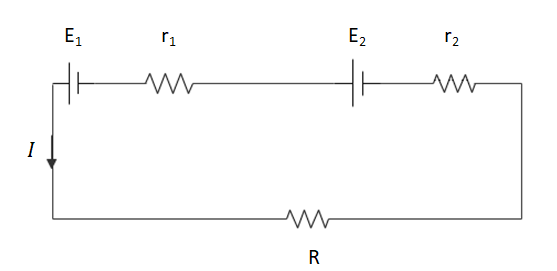
As given in the question, we have two cells of emf E1 and E2 having internal resistances of r1 and r2 respectively. These emf’s are connected in series to an external resistance R.
To find the effective current flowing through the circuit, we will use the Ohm’s law, that is V=IR. Hence, in this case the Ohm’s law becomes, Eeff=E1+E2=Ieff(Reff).
The Reff is given by the net series resistance in the circuit. Therefore Reff is, Reff=r1+r2+R.
Therefore, substituting in this value in the previous equation, we get, E1+E2=Ieff(r1+r2+R)⇒Ieff=r1+r2+RE1+E2.
As given in the problem, both the cells have the same emf, hence E1 =E2=E.
Therefore, the equation becomes, Ieff=r1+r2+R2E. This is the effective current value in the circuit.
We know that the terminal voltage across the cell E1is zero. The terminal potential across the cell E1is given by, Vterminal=E1−Ieffr1⇒0=E1−Ieffr1⇒E1=Ieffr1.
Therefore, substituting in the value of effective current into the above equation we get, E=r1+r2+R2E(r1)⇒r1+r2+R=2r1⇒R=r1−r2.
Hence, the resistance value of the external resistance R=r1−r2.
So, option C is correct here.
Note: The terminal voltage is the voltage across the cell with emf E1 can be understood as the potential drop across the cell containing the emf of potential E1 and having internal resistance r1. This terminal voltage will be recorded, if you connect a voltmeter across the two terminals of the cell E1.
Additionally, it must be known every cell has some internal resistance produced during the manufacturing itself. A cell having zero internal resistance is an ideal concept, which doesn’t work in the real world.
