Question

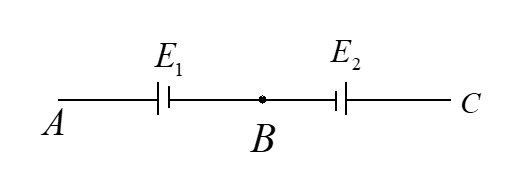
Two cells of emf ${E_1}$ and ${E_2}$( ${E_1}$>${E_2}$) are connected shown in figure. When a potentiometer is connected between A and B, the balancing length of the potentiometer wire is $300cm$. On connecting the same potentiometer between A and C, the balancing length is $100cm$. The ratio $\dfrac{{{E_1}}}{{{E_2}}}$ is:
A. $3:1$
B. $1:3$
C. $2:3$
D. $3:2$

Answer 1

Consider the balancing length of the wire and calculating the potential difference along the potentiometer wire will be helpful to solve the given problem.

Formula used:
$E \propto L$
The balancing condition:
$\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{l_1}}}{{{l_2}}}$
Where,
${E_1}$, ${E_2}$ are emfs of two cells.
${l_1}$, ${l_2}$ are the lengths of the potentiometer wire.

Complete step by step answer:
In the question it is given that emf of two cells is connected in the potentiometer.
The ratio of the potential difference across the potentiometer wire is directly proportional to the length along the potentiometer wire. That is
$E \propto L$

The balancing length of the potentiometer wire is $300cm$, when the potentiometer is connected between A and B.
We can use the balancing condition to find the ratio
$\Rightarrow \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{l_1}}}{{{l_2}}}$
We can write the ${E_2}$ as ${E_1} - {E_2}$ and we can substitute the values of the lengths in the given formula.
$\Rightarrow \dfrac{{{E_1}}}{{{E_1} - {E_2}}} = \dfrac{{300}}{{100}}$
Where ${E_1} \propto 300$ and ${E_1} - {E_2} \propto 100$.
We can write the given equation after simplifying the equation by using the division.
$\Rightarrow \dfrac{{{E_1}}}{{{E_1} - {E_2}}} = \dfrac{3}{1}$

Now we can use the cross multiplication, we get,
$\Rightarrow {E_1} = 3({E_1} - {E_2})$
We can multiply the $3$ inside with the bracket terms. We get,
$\Rightarrow {E_1} = 3{E_1} - 3{E_2}$

We can rearrange them by bringing the same terms into one side. We get,
$\Rightarrow 3{E_1} - {E_1} = 3{E_2}$
$\Rightarrow 2{E_1} = 3{E_2}$
$\Rightarrow \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{3}{2}$
$\therefore {E_1}:{E_2} = 3:2$
When we connect the same potentiometer across A and C with the length of $100cm$ ,the ratio of the emfs is measured as $3:2$.

Hence, the correct answer is option (D).

Note: The potential across any portion of the wire is always directly proportional to the length of the wire that has the cross sectional area and the current flow is constant.
The resistor that has either sliding or the rotating contact along with three terminals that tends to form an adjustable voltage divider is known as Potentiometer.
We can use the potentiometer as a rheostat by converting into only two terminals with wiper and another end.