Question

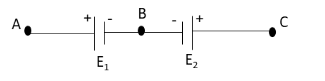
Two cells of emf ${E_1}$ and ${E_2}$ (${E_1}$,$> {E_2}$) are connected as shown in figure. When a potentiometer is connected between A and B, the balancing length of potentiometer wire is $300\,{\text{cm}}$. When the same potentiometer is connected between A and C, the balancing length is $100\,{\text{cm}}$. The ratio of ${E_1}$ and ${E_2}$ is:

A. $3:2$
B. $4:3$
C. $5:4$
D. $2:1$

Answer 1

Use the balance condition for the emf of the two cells when the potentiometer is connected between the two ends of the wire in which the cell is connected. This condition gives the relation between the emfs of the two cells and the balancing lengths for the two cells when the potentiometer is connected between the two ends of the wire in which the cell is connected.

Formula used:
The balance condition for the emf of the two cells and their balancing lengths is
$\dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{{L_1}}}{{{L_2}}}$ …… (1)
Here, ${E_1}$ is the emf of first cell, ${E_2}$ is the emf of second cell, ${L_1}$ is the balancing length for the first cell and ${L_2}$ is the balancing length for the second cell.

Complete step by step answer:
We have given that the two cells ${E_1}$ and ${E_2}$ are connected as shown in the figure. When the potentiometer is connected between points A and B, the balancing length ${L_{AB}}$ is $300\,{\text{cm}}$ and when the potentiometer is connected between points A and C, the balancing length ${L_{AC}}$ is $100\,{\text{cm}}$.
${L_{AB}} = 300\,{\text{cm}}$
$\Rightarrow{L_{AC}} = 100\,{\text{cm}}$
The emf between the points A and B is ${E_1}$.

The emf between the points A and C is the difference of the two emfs of the cells. Since the emf ${E_1}$ is greater than the emf ${E_2}$, this difference of these two cells is ${E_1} - {E_2}$.
Hence, the balance condition (1) for the present case becomes
$\dfrac{{{E_1}}}{{{E_1} - {E_2}}} = \dfrac{{{L_{AB}}}}{{{L_{AC}}}}$

Substitute $300\,{\text{cm}}$ for ${L_{AB}}$ and $100\,{\text{cm}}$ for ${L_{AC}}$ in the above equation.
$\dfrac{{{E_1}}}{{{E_1} - {E_2}}} = \dfrac{{300\,{\text{cm}}}}{{100\,{\text{cm}}}}$
$\Rightarrow 100{E_1} = 300{E_1} - 300{E_2}$
$\Rightarrow 100{E_1} - 300{E_1} = - 300{E_2}$
$\Rightarrow - 200{E_1} = 300{E_2}$
Rearrange the above equation for $\dfrac{{{E_1}}}{{{E_2}}}$.
$\Rightarrow \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{300}}{{200}}$
$\therefore \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{3}{2}$
Therefore, the ratio of the two emfs ${E_1}$ and ${E_2}$ is 3:2.

Hence, the correct option is A.

Note: The students may take the resultant emf between the two points A and C as the emf of the second cell as ${E_2}$. But the students should keep in mind that the opposite terminals of the two cells are connected to each other. Hence, the resultant emf between points A and C is the difference of the two cells.