Question

Two cells of emf $4V$ and $2V$, and internal resistance $2\Omega$ and $1\Omega$ respectively are connected in parallel so as to send the current in the same direction through an external resistance of $10\Omega$. Find the potential difference across the $10\Omega$ resistor.

Answer 1

The given problem is an example of grouping of two cells in parallel. Two cells are said to be connected in parallel between two points, if positive terminals of both the cells are connected to the one point and negative terminals of both the cells are connected to the other point.

Complete step by step solution:
Step 1:

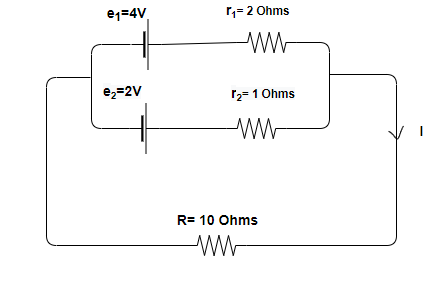
As shown in the above circuit, emfs of the given cells are $\mathop e\nolimits_1$ and $\mathop e\nolimits_2$ respectively. And internal resistances of these given cells are $\mathop r\nolimits_1$ and $\mathop r\nolimits_2$ respectively.
Let the current flowing in the circuit because of the combination of these cells is $I$ .
Where $\mathop e\nolimits_1 = 4V$, $\mathop e\nolimits_2 = 2V$, $\mathop r\nolimits_1 = 2\Omega$ , and $\mathop r\nolimits_2 = 1\Omega$.
And the external resistance is given by $R = 10\Omega$.

Step 2:

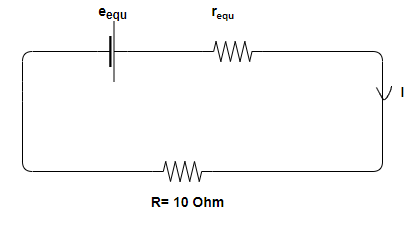
As shown in the above figure that the given circuit in step 1 that is a parallel combination of two cells can be replaced by a single cell of equivalent emf of $\mathop e\nolimits_{equ}$ between the two given points and internal resistance that is equivalent resistance $\mathop r\nolimits_{equ}$.
For the given circuit $\mathop r\nolimits_{equ}$ can be calculated by the formula –
$\mathop r\nolimits_{equ} = \dfrac{{\mathop r\nolimits_1 \mathop r\nolimits_2 }}{{\mathop r\nolimits_1 + \mathop r\nolimits_2 }}$; putting the values of $\mathop r\nolimits_1$ and $\mathop r\nolimits_2$ in this equation
$\mathop r\nolimits_{equ} = \dfrac{{2 \times 1}}{{2 + 1}}$
$\mathop r\nolimits_{equ} = \dfrac{2}{3}\Omega$..................(1)
We know that the relationship between voltage $V$, total current $I$, and resistance $R$ is given by Ohm's Law i.e., . So, using this relationship for the same given circuit $\mathop e\nolimits_{equ}$ (i.e., voltage $V$ ) can be calculated by the formula –
$\mathop e\nolimits_{equ} = \left( {\dfrac{{\mathop e\nolimits_1 }}{{\mathop r\nolimits_1 }} + \dfrac{{\mathop e\nolimits_2 }}{{\mathop r\nolimits_2 }}} \right)\mathop r\nolimits_{equ}$; putting the values of $\mathop e\nolimits_1$ and $\mathop e\nolimits_2$ , and $\mathop r\nolimits_{equ}$ in this equation
$\mathop e\nolimits_{equ} = \left( {\dfrac{4}{2} + \dfrac{2}{1}} \right)\dfrac{2}{3}$
$\mathop e\nolimits_{equ} = \dfrac{8}{3}V$...................(2)
Step 3: Now potential difference across the $R = 10\Omega$ (let $\mathop E\nolimits_R$) can be calculated by voltage divider rule as given follows –
$\mathop E\nolimits_R = \left( {\dfrac{R}{{R + \mathop r\nolimits_{equ} }}} \right)\mathop e\nolimits_{equ}$
Now, using the values of $\mathop e\nolimits_{equ}$, $\mathop r\nolimits_{equ}$, and $R$ from above calculations, we will get
$\mathop E\nolimits_R = \left( {\dfrac{10}{{10 + {2/3}}}} \right)\dfrac{8}{3}$
$\mathop E\nolimits_R = \left( {\dfrac{{10 \times 3}}{{30 + 2}}} \right)\dfrac{8}{3}$; on simplifying the above equation
$\mathop E\nolimits_R = \dfrac{{10 \times 8}}{{32}}$
$\mathop E\nolimits_R = 2.5V$

The potential difference across the given resistance $R = 10\Omega$ is $\mathop E\nolimits_R = 2.5V$.

Note: If $n$ number of identical cells are connected in parallel of emfs $e$ and internal resistance $r$, then internal equivalent resistance is given by –
$\mathop r\nolimits_{equ} = \dfrac{r}{n}$.
In a parallel combination of identical cells, the effective /equivalent emf in the circuit is equal to the emf due to a single cell i.e., $\mathop e\nolimits_{equ} = e$.