Question

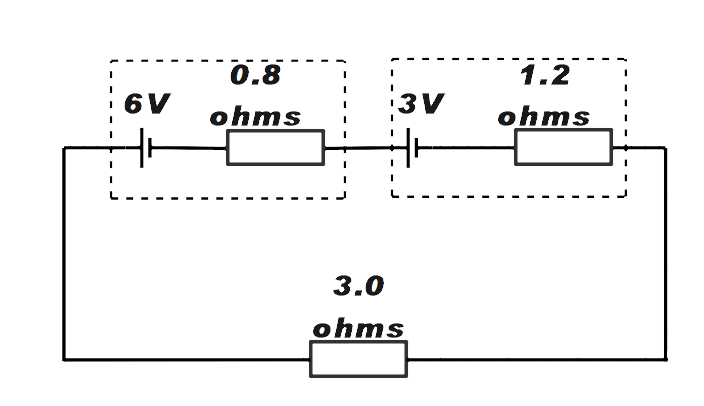
Two cells are connected to a load resistor of resistance 3.0 $\Omega$. The electromotive force (emf). and the internal resistance of each of the cells is shown. What is the current in the load resistor?

Answer 1

In this question we have been asked to calculate the current in the load resistor in the given circuit. The given circuit consists of two cells with given emf and internal resistance are connected to a load resistor. Now, we know that the voltage difference across a loop of a circuit is always zero. This is the statement of Kirchhoff’s voltage law. Therefore, we shall use Kirchhoff’s voltage law or Kirchhoff’s second rule to calculate the current in the load resistor.

Complete step-by-step answer:
It is given that two cells are connected to a load resistor of 3 Ohms. From the given figure, the emf and internal resistor of first cell will be given by,
${{V}_{1}}=6V$ and ${{R}_{1}}=0.8\Omega$ …………… (1)
Similarly, for second cell,
${{V}_{2}}=3V$ and ${{R}_{2}}=1.2\Omega$ ………….. (2)
Now, let I be the current flowing in the circuit and resistance of load resistor be ${{R}_{3}}$
Therefore, using Kirchhoff’s loop rule in anticlockwise direction,
We get,
${{R}_{2}}I+{{V}_{2}}-{{R}_{1}}I+{{V}_{1}}-{{R}_{3}}I=0$
After substituting the given values,
We get,
$-1.2I+3-0.8I+6-3I=0$
On solving,
We get,
$I=1.8A$
Therefore, the current flowing through the load resistor is 1.8 Amperes.

Note: The Kirchhoff’s loop rule also known as Kirchhoff’s voltage law states that the sum of voltage difference across a complete loop is always zero. It means that the voltage drop across a loop is zero. This law is similar to conservation of energy in terms of electric potential. The internal resistance is the opposition to the flow of current that is offered by the cells and batteries themselves.