Question

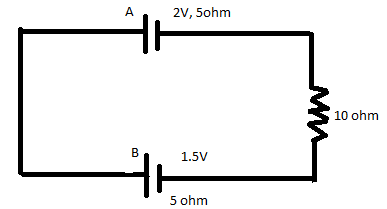
Two cells A and B of emf $2\,{\text{V}}$ and $1.5\,{\text{V}}$ respectively, are connected as shown in figure through an external resistance $10\,\Omega$. The internal resistance of each cell is $5\,\Omega$. The potential difference ${E_A}$ and ${E_B}$ across the terminals of the cells A and B respectively are:

A.${E_A} = 2.0\,{\text{V}},\,{E_B} = 1.5\,{\text{V}}$
B.${E_A} = 2.125\,{\text{V}},\,{E_B} = 1.375\,{\text{V}}$
C.${E_A} = 1.875\,{\text{V}},\,{E_B} = 1.625\,{\text{V}}$
D.${E_A} = 1.875\,{\text{V}},\,{E_B} = 1.375\,{\text{V}}$

Answer 1

First of all, we will find the net emf of the circuit and net resistance. Then we will find the net current flowing through the circuit. After that will find the potential difference by putting the values and manipulating accordingly.

Complete step by step answer:
In the given problem,
The first cell, labelled as A has an electromotive force of $2\,{\text{V}}$ and an internal resistance of $5\,\Omega$ .
The second cell, labelled as B has an electromotive force of $1.5\,{\text{V}}$ and an internal resistance of $5\,\Omega$ too.
An external resistance of $10\,\Omega$ is connected in the series with the two cells.

First of all, we will find the expression for net electromotive force in the circuit:
${E_{net}} = {E_A} - {E_B}$ …… (1)
Where,
${E_{net}}$ indicates net electromotive force in the circuit.
${E_A}$ indicates electromotive force of cell A.
${E_B}$ indicates electromotive force of cell B.
Substituting the required values in the equation (1), we get:
{E_{net}} = {E_A} - {E_B} \\\ \implies {E_{net}} = 2 - 1.5 \\\ \implies {E_{net}} = 0.5\,{\text{V}} \\\
The net electromotive force comes out to be $0.5\,{\text{V}}$ .

Now, we will find the net resistance in the circuit:
Net resistance in the circuit is the sum of the internal resistance of each cell along with the external resistance connected in the circuit, in series with the two cells.
It is given by:
${R_{net}} = {r_A} + {r_B} + R$ …… (2)
Where,
${R_{net}}$ indicates the total or net resistance in the circuit.
${r_A}$ indicates the internal resistance of cell A.
${r_B}$ indicates the internal resistance of cell B.
$R$ indicates the external resistance connected in the circuit.
Substituting the required values in the equation (2), we get:
{R_{net}} = {r_A} + {r_B} + R \\\ \implies {R_{net}} = 5 + 5 + 10 \\\ \implies {R_{net}} = 20\,\Omega \\\
The total or net resistance comes out to be $20\,\Omega$ .

We know, the formula which relates current, potential difference and resistance is as follows:
$I = \dfrac{{{E_{net}}}}{{{R_{net}}}}$
Now, substituting the required values in the above equation, we get:
I = \dfrac{{0.5}}{{20}}\,{\text{A}} \\\ \implies I = 0.025\,{\text{A}} \\\
The total current flowing in the circuit is $0.025\,{\text{A}}$ .
Now,
The potential difference across cell A is given by:
{V_A} = {E_A} - I{r_A} \\\ \implies {V_A} = 2 - 0.025 \times 5 \\\ \implies {V_A} = 2 - 0.125 \\\ \therefore {V_A} = 1.875\,{\text{V}} \\\

The potential difference across cell B is given by:
{V_B} = {E_B} + I{r_B} \\\ \implies {V_B} = 1.5 + 0.025 \times 5 \\\ \implies {V_B} = 1.5 + 0.125 \\\ \therefore {V_B} = 1.625\,{\text{V}} \\\

So, the correct answer is “Option C”.

Note:
This problem is based on Ohm’s law. While solving this problem, keep in mind that the total resistance of the circuit is not just $10\,\Omega$, rather the internal resistances should also be counted, as they also contribute. While finding the potential difference across the terminals of B, you must add the potential of the cell emf of the cell and the terminal voltage.