Question

Two car's 'A' and 'B' are moving with a speed of 15 m/s and 5 m/s and acceleration of the car is 1 m/s² and 6 m/s² respectively. Then the minimum seperation between them is

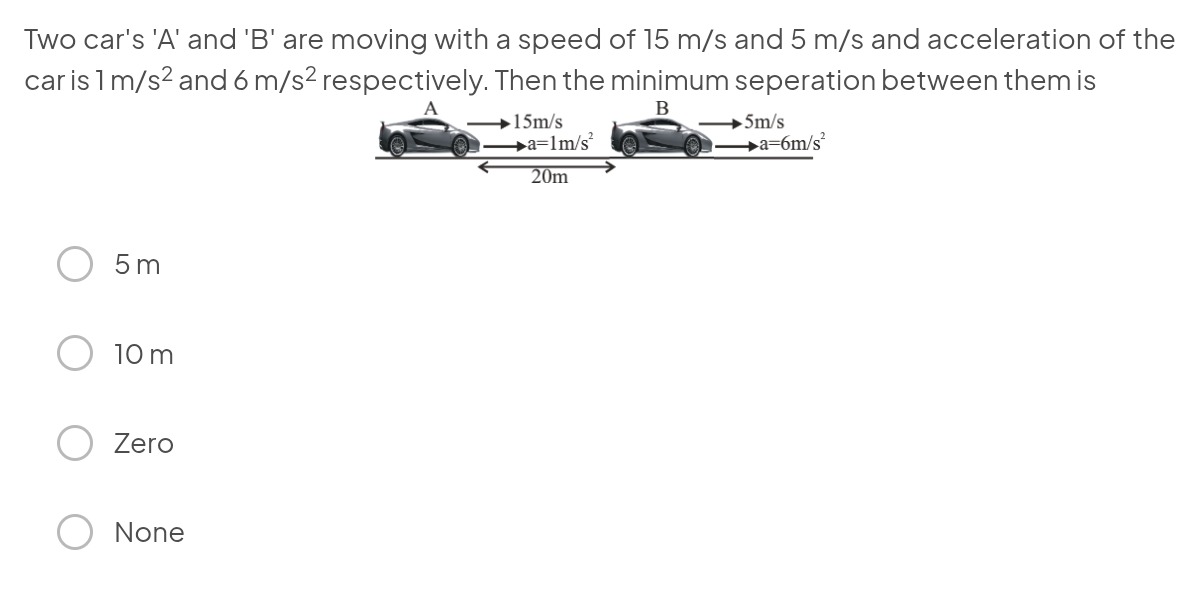
• A. 5 m
• B. 10 m
• C. Zero
• D. None

Answer 1

Answer: (B)

10 m

Answer 2

The position of car A at time $t$ is given by $x_A(t) = x_{A0} + v_{A0}t + \frac{1}{2}a_At^2$. The position of car B at time $t$ is given by $x_B(t) = x_{B0} + v_{B0}t + \frac{1}{2}a_Bt^2$. Let car A be at the origin initially, so $x_{A0} = 0$. Then car B is at $x_{B0} = 20$ m. Given $v_{A0} = 15$ m/s, $a_A = 1$ m/s², $v_{B0} = 5$ m/s, $a_B = 6$ m/s². The separation between the cars is $S(t) = x_B(t) - x_A(t)$. $S(t) = (20 + 5t + \frac{1}{2}(6)t^2) - (0 + 15t + \frac{1}{2}(1)t^2)$ $S(t) = 20 + 5t + 3t^2 - 15t - \frac{1}{2}t^2$ $S(t) = 20 - 10t + \frac{5}{2}t^2$

To find the minimum separation, we find the time $t$ when the derivative of $S(t)$ with respect to $t$ is zero. $\frac{dS}{dt} = -10 + 2(\frac{5}{2})t = -10 + 5t$ Setting $\frac{dS}{dt} = 0$: $-10 + 5t = 0 \implies 5t = 10 \implies t = 2$ s.

Now, substitute $t=2$ s into the separation equation to find the minimum separation: $S_{min} = S(2) = 20 - 10(2) + \frac{5}{2}(2)^2$ $S_{min} = 20 - 20 + \frac{5}{2}(4)$ $S_{min} = 0 + 10 = 10$ m.

Alternatively, using relative motion: The relative velocity of car B with respect to car A is $v_{rel}(t) = v_{B0} - v_{A0} + (a_B - a_A)t$. $v_{rel}(t) = (5 - 15) + (6 - 1)t = -10 + 5t$. The relative acceleration is $a_{rel} = a_B - a_A = 5$ m/s². The initial separation is $S_0 = 20$ m. The relative position is $S(t) = S_0 + v_{rel,0}t + \frac{1}{2}a_{rel}t^2 = 20 - 10t + \frac{1}{2}(5)t^2$. The minimum separation occurs when $v_{rel}(t) = 0$, which gives $t = 2$ s. Substituting $t=2$ s into $S(t)$ gives $S_{min} = 10$ m.