Question
Question: Two car A and B start racing at the same time on a flat race track which consists of two straight se...
Two car A and B start racing at the same time on a flat race track which consists of two straight sections each of length 100πand one circular section as is the Fig. The rule of the race is that each car must travel at a constant speed at all times without ever skidding. Then:
A. Car A completes its journey before car B.
B. Both cars complete the journey at the same time.
C. Velocity of car A is greater than that of car B.
D. Car B completes its journey before car A.
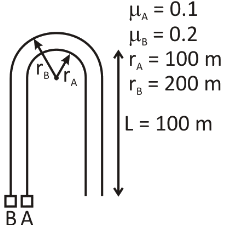
Solution
First of all, we will find the centripetal and the centrifugal forces, which acts on the two cars. Both of them will be equal and we will equate. We will find the velocity, distance covered and the time taken by each car. After that we will compare the results.
Formula used:
The formula that gives the centrifugal force is:
Fcp=μmg
Where,
μ indicates coefficient of friction.
m indicates mass of the body.
g indicates acceleration due to gravity.
Centripetal force can be written as:
Fcg=rmv2
Where,
m indicates mass of the body.
r indicates the radius of the path.
v indicates velocity.
Complete step by step answer:
If the condition is taken for the cars not to slide, then the centripetal force should be equal to centrifugal force. Then, mathematically it can be written as:
μmg=rmv2
Rearranging the above equation:
\mu mg = \dfrac{{m{v^2}}}{r} \\\
\Rightarrow \mu \times r \times g = {v^2} \\\
\Rightarrow v = \sqrt {\mu \times r \times g} \\\
Hence, the expression for velocity is:
v=μ×r×g ...... (1)
The curved path is semi-circular.
For the car A, the velocity can be found out by substituting μ=0.1, r=100m and g=10m/s2 in equation (1):
v = \sqrt {\mu \times r \times g} \\\
\Rightarrow v = \sqrt {0.1 \times 100 \times 10} \\\
\Rightarrow v = \sqrt {\dfrac{1}{{10}} \times 100 \times 10} \\\
\Rightarrow v = \sqrt {100} \\\
⇒v=10m/s
Total distance travelled by the car A is the summation of the distance of two straight sections and curved distance i.e.
Total distance (S):
S = 2 \times 100\pi + 100\pi \\\
\Rightarrow S = 200\pi + 100\pi \\\
\Rightarrow S = 300\pi \\\
The time taken is given by the formula:
{t_{\text{A}}} = \dfrac{S}{v} \\\
\Rightarrow {t_{\text{A}}} = \dfrac{{300\pi }}{{10}} \\\
\Rightarrow {t_{\text{A}}} = 30\pi \,{\text{sec}} \\\
For the car B,
The velocity can be found out by substituting μ=0.2, r=200m and g=10m/s2 in equation (1):
v = \sqrt {\mu \times r \times g} \\\
\Rightarrow v = \sqrt {0.2 \times 200 \times 10} \\\
\Rightarrow v = \sqrt {\dfrac{2}{{10}} \times 200 \times 10} \\\
\Rightarrow v = \sqrt {400} \\\
⇒v=20m/s
Total distance travelled by the car A is the summation of the distance of two straight sections and curved distance i.e, total distance (S):
S = 2 \times 100\pi + 200\pi \\\
\Rightarrow S = 200\pi + 200\pi \\\
\Rightarrow S = 400\pi \\\
The time taken is given by the formula:
{t_{\text{B}}} = \dfrac{S}{v} \\\
\Rightarrow {t_{\text{B}}} = \dfrac{{400\pi }}{{20}} \\\
\Rightarrow {t_{\text{B}}} = 20\pi \,{\text{sec}} \\\
Since, the time taken by car A is more than car B. So, car B completes its journey before car A.
The correct option is D.
Note: While solving this problem, most of the students seem to have a confusion regarding the total distance covered by each car. The net distance travelled by each car is the summation of the longitudinal distance and the circumference of the semi-circle. Lower the time taken, faster it moves.
