Question

Two capacitors having capacitance ${C_1}$and ${C_2}$ are charged with 120V and 200V batteries respectively. When they are connected in parallel now, it is found that the potential on each of them is zero. Then:
$(a){\text{ 8}}{{\text{C}}_1} = 5{C_2} \\\ (b){\text{ 9}}{{\text{C}}_1} = 5{C_2} \\\ (c){\text{ 3}}{{\text{C}}_1} = 5{C_2} \\\ (d){\text{ 5}}{{\text{C}}_1} = 3{C_2} \\\$

Answer 1

Hint: In this question use the relationship between the capacitance, charge and potential on a capacitor that is $Q = CV$. Use the constraints given in the question to find the charge onto the two capacitors. Then use the fact that since potential is found to be zero therefore the capacitors must be connected in phase opposition (i.e. positive sign connected to positive and negative sign connected to negative) that is ${Q_1} - {Q_2} = 0$. This will help get the right answer to this problem statement.

Complete step-by-step solution:

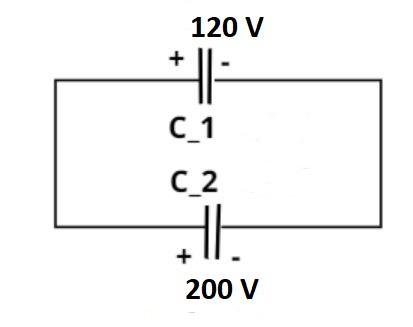
As we know that the charge stored on the capacitor is the product of individual capacitance and the voltage stored in the capacitor.
$\Rightarrow Q = CV$.................. (1)
Where, Q = charge, C = capacitance and V = voltage.
Now let the capacitance of first capacitor be ${C_1}$ and the capacitance of second capacitor be ${C_2}$
Charged voltages of the first and second capacitor are 120V and 200V.
So the charges on the first and second capacitor are
$\Rightarrow {Q_1} = 120{C_1}$ Coulomb
And
$\Rightarrow {Q_2} = 200{C_2}$Coulomb.
Now it is given that they are connected in parallel and it is found that the potential on each of them is zero.
So from equation (1) if the potential or voltage on each of them is zero then the charge on each of them will be zero.
It is only possible when they connected in phase opposition (i.e. positive sign connected to positive and negative sign connected to negative) as shown in figure, such that ${Q_1} - {Q_2} = 0$
Now substitute the values in above equation we have,
$\Rightarrow {Q_1} - {Q_2} = 0$
$\Rightarrow 120{C_1} - 200{C_2} = 0$
Now simplify this we have,
$\Rightarrow 120{C_1} = 200{C_2}$
Divide by 40 throughout we have,
$\Rightarrow 3{C_1} = 5{C_2}$
So this is the required relation between ${C_1}$ and ${C_2}$ i.e. first and second capacitor.
Hence option (C) is the correct answer.

Note – The parallel combinatory of the capacitors is exactly equivalent to that series connection of the resistors that is ${C_{eq}} = {C_1} + {C_2}$, it is advised to remember the direct relationship that is $q = cv$. A parallel plate capacitor is formed by charge parallel plates which may have dielectric or even air filled in between the plates. These plates are separated by some distance d and if A is the area of cross-section of the plates then capacitance C is given by $C = \dfrac{{{ \in _0}A}}{d}$. This information is quite useful while dealing with problems involving capacitors.