Question

Two capacitors each having a capacitor $C$ and breakdown voltage $V$ are joined in series. The effective capacitance and maximum working voltage of the combination is:
(A) $2C,2V$
(B) $\dfrac{C}{2},\dfrac{V}{2}$
(C) $2C,V$
(D) $\dfrac{C}{2},2V$

Answer 1

We know for a given capacitor, charge $Q$ on a capacitor is proportional to potential difference $V$, between the plates.
$Q = CV$
And, for series combination charges on capacitors remain the same.

Complete Step by Step Answer
Figure, shows two capacitors connected in series. The capacitance is $C$ and $C$.

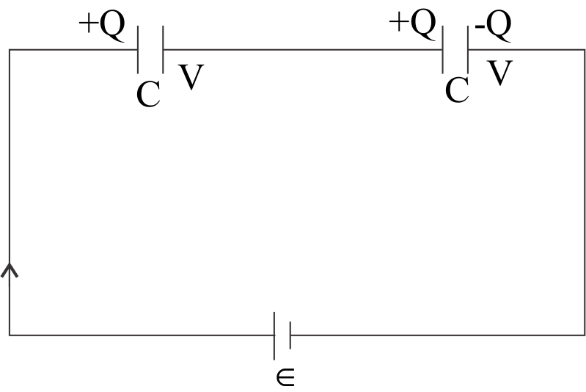
Now, let us take the potential of the right plate of the second plate to be zero. The potential of the left plate of the first capacitor is $E$. Since, the breakdown voltage of capacitors is $V$. Therefore capacitor $1$,
$E - V = \dfrac{Q}{C}...........(i)$
Similarly, for other capacitor,
$V - 0 = \dfrac{Q}{C}...........(ii)$
Adding equation $(i)$ and $(ii)$
$E = Q\left( {\dfrac{1}{C} + \dfrac{1}{C}} \right)\,.........\,(iii)$
If the equivalent capacitance of the combination is ${C_{eq}}$.
${C_{eq}} = \dfrac{Q}{E}\,..........\,(iv)$
Using equation $(iii)$ and $(iv)$ we get,
${C_{eq}} = \dfrac{C}{2}\,$
And, the maximum working voltage is $E$.
Hence, $E = V + V = 2V$

Hence, Option (D) is correct

Note:
Charge on series combination remains same but voltage changes with respect to the capacitance whereas voltage on parallel combination remains same but charge varies in accordance to capacitance.