Solveeit Logo
Login

Question

Question: Two capacitors \(C_1\) of \(4\mu F\) and \(C_2\) of \(1\mu F\) are connected in series with the batt...

Two capacitors C1C_1 of 4μF4\mu F and C2C_2 of 1μF1\mu F are connected in series with the battery. If total potential difference across the two capacitors is 200 volts then the ratio of potential difference across capacitor to that across capacitor is:
a) 1:2
b) 2:1
c) 1:4
d) 4:1

Explanation

Solution

The capacitors connected in series will have the same amount of charging current flowing through them. The electrical charge stored in the capacitors will be the same, as the charge stored by a plate of a particular capacitor is equal and opposite to that of the adjacent capacitor plate. The charge stored within the capacitor can be determined by using:
Q=C×VQ=C\times V

Complete Solution:
The problem can be depicted by the circuit diagram shown below:

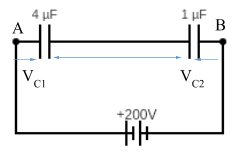
Capacitor connected in series must have same charge, therefore QTotal=QC1=QC2{{Q}_{Total}}={{Q}_{C1}}={{Q}_{C2}}

Applying Kirchhoff’s Voltage law in the above circuit will give us:
VAB=VC1+VC2=200V{{V}_{AB}}={{V}_{C1}}+{{V}_{C2}}=200V

Hence, Voltage across each capacitor will be:
VC1=QtotalC1{{V}_{C1}}=\dfrac{{{Q}_{total}}}{{{C}_{1}}} ------(1)
And,
VC2=QtotalC2{{V}_{C2}}=\dfrac{{{Q}_{total}}}{{{C}_{2}}} ------(2)

Dividing equation 1 by 2 will give us: VC2VC1=C1C2\dfrac{{{V}_{C2}}}{{{V}_{C1}}}=\dfrac{{{C}_{1}}}{{{C}_{2}}}

Putting the values of C1{{C}_{1}} and C2{{C}_{2}},
VC2VC1=41\dfrac{{{V}_{C2}}}{{{V}_{C1}}}=\dfrac{4}{1}

Hence, the ratio of potential difference across capacitor C2{{C}_{2}} to that across capacitor C1{{C}_{1}} is 4:1.

Note:
Always make sure that what ratio you have been asked for, is that ratio of 1st with respect to 2nd or it is ratio of 2nd with respect to 1st. most of the time both the options are given in the question. We can also find out the ratio by evaluating the total electrical charge which will be stored within the capacitors by evaluating total capacitance using:_
1C=1C1+1C2\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}
C=45μFC=\dfrac{4}{5}\mu F
Total charge, Qtotal{{Q}_{total}} =C×V=80μCC\times V=80\mu C
Hence, Voltage acrossC1{{C}_{1}} and C2{{C}_{2}}, using equation 1 and 2, will be 20 V and 80 V, respectively, which will give us the ratio of potential difference across C2{{C}_{2}} to C1{{C}_{1}} as 4:1.