Question

Two C and D intersect at two different points, where C is $y={{x}^{2}}-3$ and D is $y=k{{x}^{2}}$. The intersection at which the x value is positive designated as point A, and $x=a$ at this intersection. The tangent line l at A to the curve D intersects curve C at point B, other than A. If x-value of point B is 1, then a=
(a) 1
(b) 2
(c) 3
(d) 4

Answer 1

We start solving the problem by drawing all the information and find the value of y co-ordinate of point B using the fact that point B lies on the curve C. We then find the slope of the tangent to the curve D at point A using the fact that the slope of the tangent to ant y at the given point $\left( {{x}_{1}},{{y}_{1}} \right)$ is ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$. We then find the relation between k and a using the fact that point A lies on both curves C and D. We find the slope of the tangent using the formula $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and substitute the relation in it to get the value of a.

Complete step by step answer:
According to the we have two curves C and D bearing equations $y={{x}^{2}}-3$ and $y=k{{x}^{2}}$ intersects at two points. One of the intersection points is A, where the value of x co-ordinate is positive and the value is $x=a$. The tangent at point A to the curve D intersects the curve C at point B which has value of x co-ordinate 1. We need to find the value of a.
Let us draw the given information to get a better view.

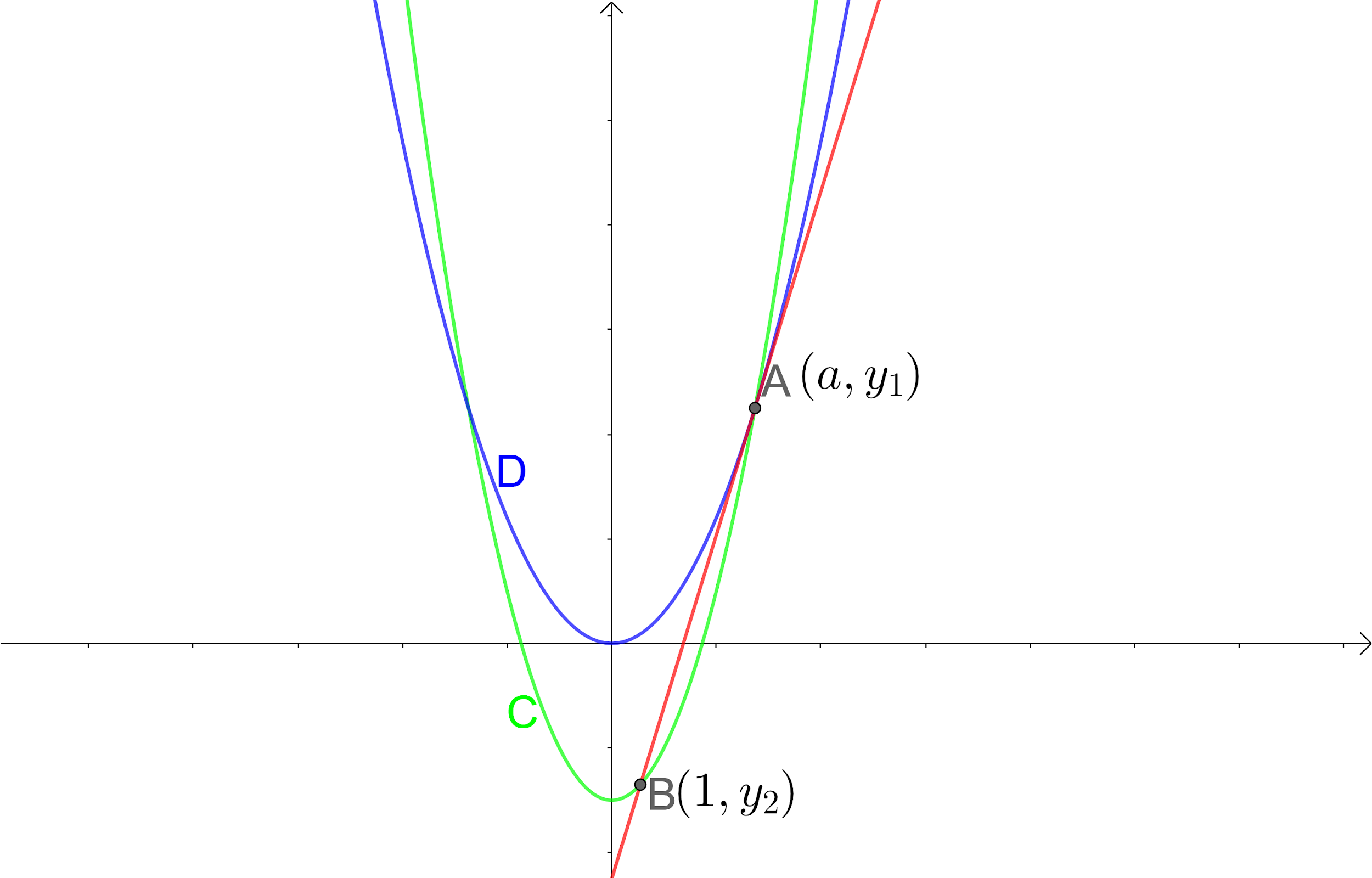
Let us assume the value of y co-ordinate of the point A be ${{y}_{1}}$ and the value of the y co-ordinate of the point B be ${{y}_{2}}$.
So, we get the points A and B as $\left( a,{{y}_{1}} \right)$ and $\left( 1,{{y}_{2}} \right)$.
From the figure we can see that the point $B\left( 1,{{y}_{2}} \right)$ lies on the curve $y={{x}^{2}}-3$. Let us substitute the point in the equation.
$\Rightarrow {{y}_{2}}={{1}^{2}}-3$.
$\Rightarrow {{y}_{2}}=1-3$.
$\Rightarrow {{y}_{2}}=-2$.
So, the co-ordinates of the point B is $\left( 1,-2 \right)$ ---(1).
We know that the slope of the tangent to ant y at the given point $\left( {{x}_{1}},{{y}_{1}} \right)$ is ${{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}$. So, we need to find the slope of the tangent to the curve $y=k{{x}^{2}}$ at the point A$\left( a,{{y}_{1}} \right)$.
So, we have $y=k{{x}^{2}}$. Let us differentiate both sides with respect to x.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( k{{x}^{2}} \right)$.
We know that $\dfrac{d}{dx}\left( af\left( x \right) \right)=a\dfrac{d}{dx}\left( f\left( x \right) \right)$.
$\Rightarrow \dfrac{dy}{dx}=k\dfrac{d}{dx}\left( {{x}^{2}} \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$.
$\Rightarrow \dfrac{dy}{dx}=k\left( 2x \right)$.
$\Rightarrow \dfrac{dy}{dx}=2kx$.
Let us substitute the point A$\left( a,{{y}_{1}} \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( a,{{y}_{1}} \right)}}=2k\left( a \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( a,{{y}_{1}} \right)}}=2ka$ ---(2).
We have point A$\left( a,{{y}_{1}} \right)$ lies on both the curves C $y={{x}^{2}}-3$ and D $y=k{{x}^{2}}$. Let us substitute in those curves.
So, we have ${{y}_{1}}={{a}^{2}}-3$ ---(3).
We also have ${{y}_{1}}=k{{a}^{2}}$ ---(4).
From (3) and (4), we have ${{a}^{2}}-3=k{{a}^{2}}$.
$a-\dfrac{3}{a}=ka$ ---(5).
We have the tangent at A$\left( a,{{y}_{1}} \right)$ passing through the point B$\left( 1,-2 \right)$.
We know that slope of the line passing through the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
So, the slope of the tangent is $\dfrac{{{y}_{1}}-\left( -2 \right)}{a-1}$. But the slope of the tangent is $2ka$.
So, we have $\dfrac{{{y}_{1}}+2}{a-1}=2ka$.
From equations (3) and (5),
$\Rightarrow \dfrac{{{a}^{2}}-3+2}{a-1}=2\left( a-\dfrac{3}{a} \right)$.
$\Rightarrow \dfrac{{{a}^{2}}-1}{a-1}=2\left( \dfrac{{{a}^{2}}-3}{a} \right)$.
$\Rightarrow a+1=\dfrac{2{{a}^{2}}-6}{a}$.
$\Rightarrow {{a}^{2}}+a=2{{a}^{2}}-6$.
$\Rightarrow 2{{a}^{2}}-{{a}^{2}}-a-6=0$.
$\Rightarrow {{a}^{2}}-a-6=0$.
$\Rightarrow {{a}^{2}}-3a+2a-6=0$.
$\Rightarrow a\left( a-3 \right)+2\left( a-3 \right)=0$.
$\Rightarrow \left( a+2 \right)\left( a-3 \right)=0$.
$\Rightarrow \left( a+2 \right)=0 or \left( a-3 \right)=0$.
$\Rightarrow a=-2$ or $a=3$.
According to the problem the value of a is positive. So, we have found the value of a is 3.
∴ The value of a is 3.

So, the correct answer is “Option C”.

Note: We neglected the negative value of a as it is clearly mentioned in the problem that the value of a is positive. We can also find the value of k using the obtained value of k and get the equation of the curve D. Using the equation of the curve, we can find all related properties of the curve D like length of the latus rectum, focus, vertex. Similarly, we can expect problems to find the normal of C at point A after obtaining the value of a.