Question

Two boys $P$ and $Q$ are playing on a riverbank. $P$ plans to swim across the river directly and come back. $Q$ plans to swim downstream by a length equal to the width of the river and then come back. Both of them bet each other, claiming that the boy succeeding in less time will win. Assuming the swimming rate of both $P$ and $Q$ to the same, it can be concluded that:
A. $P$ wins
B. $Q$ wins
C. A draw takes place
D. Nothing certain can be stated.

Answer 1

You can start by calculating the velocity for boy $P$ i.e. ${V_{net}} = \sqrt {{V^2} - V_r^2}$. Then use the equation for speed i.e. $s = \dfrac{d}{t}$ to calculate the time taken by $P$ . Then first calculate the velocity and time taken by $Q$ while going downstream i.e. ${V_{down}} = V + {V_r}$ and ${t_{down}} = \dfrac{W}{{V + {V_r}}}$ respectively. Then calculate the velocity and time taken by $Q$ while going upstream i.e. ${V_{up}} = V - {V_r}$ and ${t_{up}} = \dfrac{W}{{V - {V_r}}}$ respectively. Then calculate total time taken by $Q$ in going back and forth. Then compare the time taken by $P$ and $Q$ to reach the solution.

Complete answer:
Let the width of the river be $W$ .
The distance covered in both cases is $2W$ .
Here we assume that both the boys move with a velocity $V$ when no other force is involved.
The velocity of the water in the stream is ${V_r}$ .
For $P$, we know that for the boy to cross the river directly he will have to start swimming at an angle $\theta$ as shown in the diagram below

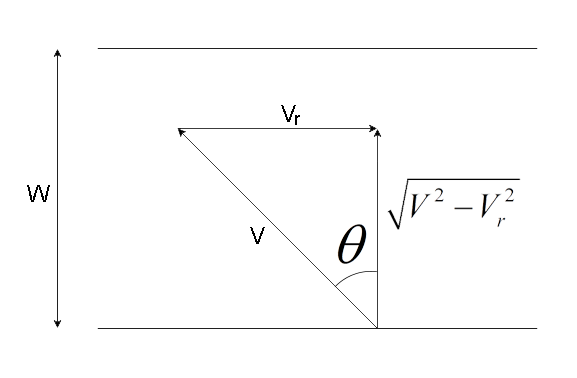
We know that the equation for speed is
$s = \dfrac{d}{t}$ (Equation 1)
$\Rightarrow t = \dfrac{d}{s}$
Here, $t =$ time
$d =$ Distance
$s =$ Speed
In this case by Pythagoras theorem
${V_{net}} = \sqrt {{V^2} - V_r^2}$
So in this equation 1 becomes
${t_P} = \dfrac{{2W}}{{\sqrt {{V^2} - V_r^2} }}$
For $Q$ , we can break down his motion in two parts.
For the part where $Q$ goes downstream the velocity becomes
${T_{down}} = V + {V_r}$
So, equation 1 here becomes
${t_{down}} = \dfrac{W}{{V + {V_r}}}$
For the part where $Q$ goes upstream
${V_{up}} = V - {V_r}$
So, equation 1 here becomes
${t_{up}} = \dfrac{W}{{V - {V_r}}}$
Total time taken by $Q$ becomes
${t_Q} = {t_{down}} + {t_{up}}$
$\Rightarrow {t_Q} = \dfrac{W}{{V + {V_r}}} + \dfrac{W}{{V - {V_r}}}$
$\Rightarrow {t_Q} = \dfrac{{W(V - {V_r}) + W(V + {V_r})}}{{{V^2} - V_r^2}}$
$\Rightarrow {t_Q} = \dfrac{{2W(V}}{{{V^2} - V_r^2}}$
We have to calculate the value of ${T_P} - {T_Q}$
${T_P} - {T_Q} = \dfrac{{2W}}{{\sqrt {{V^2} - V_r^2} }} - \dfrac{{2VW}}{{{V_2} - V_r^2}}$
${T_P} - {T_Q} = \dfrac{{2W}}{V}\left( {\dfrac{1}{{\sqrt {1 - {x^2}} }} - \dfrac{1}{{1 - {x^2}}}} \right)$ (Where $x = \dfrac{{{V_r}}}{V} < 1$ )
$\dfrac{{2W}}{{V\sqrt {1 - {x^2}} }}$ is positive and $1 - \dfrac{1}{{\sqrt {1 - {x^2}} }}$ is negative because $\dfrac{1}{{\sqrt {1 - {x^2}} }} > 1$ .
$\therefore {T_P} - {T_Q} < 0$
$\therefore {T_P} < {T_Q}$
Hence, the boy $P$ takes less time and wins.

So, the correct answer is “Option A”.

Note:
In the solution discussed above we mentioned that boy $P$ starts from one end of the river at an angle $\theta$. We assume this because if the boy did not go at an angle and just straight, he would drift away because of the force of the water in the river, and to counteract this drift he would have to start an angle $\theta$.