Question

Two boys are holding a horizontal rod of length L and weight W through its two ends. If now one of the boys suddenly leaves the rod, what is the instantaneous reaction force experienced by the other boy?
A. $\dfrac{W}{4}$
B. $\dfrac{W}{2}$
C. $\dfrac{{3W}}{4}$
D. W

Answer 1

In this question, when both the boys are holding the rod there is no motion of the rod. The system is in equilibrium. As soon as one of the boys suddenly leaves the rod, torque acts on the rod. The center of mass will have some acceleration. By balancing the equations, we can find the instantaneous reaction force.

Complete step by step answer:
Initially the two boys are holding the rod in a horizontal manner. In this position the rod is balanced. As soon as one of the boys leaves the rod, there is unbalanced force at one end of the rod. We know that when we apply force to one end of the rod there is rotational motion of the rod. Let us draw the free body diagram for the same:

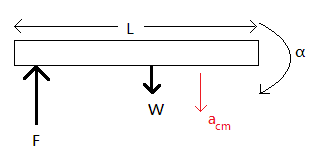
Consider, F is the force given by one boy.
W is the weight of the rod
m is the mass of the rod
L is the length of the rod
${a_{cm}}$ is the acceleration of the centre of mass of the rod
$\alpha$ is the instantaneous angular acceleration of the rod
As soon as one boy leaves the rod, torque acts on the rod and this torque $\tau$ is given as
$\tau = {\rm I}\alpha$
Where I is the moment of inertia of the rod and has value ${\rm I} = \dfrac{{m{L^2}}}{3}$
$\Rightarrow \tau = \dfrac{{m{L^2}}}{3}\alpha$
The torque acts at the centre of the rod and has force equal to the product of its mass and acceleration due to gravity
$\Rightarrow mg\dfrac{L}{2} = \dfrac{{m{L^2}}}{3}\alpha$
$\Rightarrow \dfrac{{3g}}{{2L}} = \alpha$ --equation $1$
The acceleration of the centre of the mass of the rod is given as
${a_{cm}} = \dfrac{L}{2}\alpha$ --equation $2$

The vertical linear forces on the rod are
$W - F = ma$
$\Rightarrow mg - F = m\left( {\dfrac{{3g}}{4}} \right)$
$\Rightarrow F = \dfrac{{mg}}{4}$
$\Rightarrow F = \dfrac{W}{4}$
This is the instantaneous reaction force acting on the second boy.

So, the correct answer is “Option A”.

Note:
The forces on the rod are balanced vertically.
As soon as one of the boys leaves the rod, the rod has a tendency to perform rotational motion.
The centre through to the rod performs rotational motion is known as instantaneous centre of rotation.
The rod will have linear as well as angular acceleration.