Question
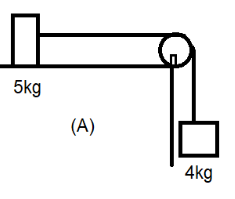
Question: Two bodies of masses \[5\;kg\] and \[4\;kg\] are arranged in two different ways as shown in fig (A) ...
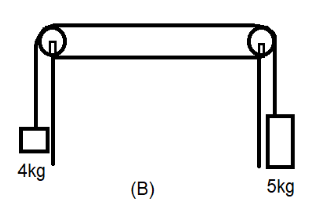
Two bodies of masses 5kg and 4kg are arranged in two different ways as shown in fig (A) and (B). If the pulleys and the table are smooth the acceleration of the 5kg body in case (A) and (B) respectively are:
A. g and 95g
B. 94g and 91g
C. 5gand 5g
D. 95g and 91g
Solution
The concept of free body diagrams are applied as there are more than two bodies that are connected together and hence all the forces that are applied on the body are taken into consideration. The concept related to Newton's Second Law of motion is applied to find the acceleration value. The total forces exerted on the block that is considered is equated to with the Newton’s law equation.
Formula used:
The formula as per the Newton’s Second Law of motion is:
a=MtotalFext
Where, a is the acceleration of the body, Mtotal is the total mass of the bodies in the system and Fext is the external forces applied on the body.
Complete step by step answer:
The first step is to identify which concept is to be applied for the given problem. From the question and the diagram it is clear that the concept of connected bodies wherein two or more than two bodies are connected to each other. The concept of free body diagrams are applied to these connected bodies to determine all the forces that are exerted on the body which may be in motion. This means that the bodies have a certain amount of acceleration associated with it in the direction of the force which is greater in magnitude.
To find out the different forces that act upon a certain object we must know the concept behind free body diagrams. A free body diagram is a diagram for each body of the system showing all the forces exerted on the body by the remaining parts of the system.We first extract the data from the given problem. Let: given, m1=5kg and m2=4kg.
When a certain number of bodies are connected together by strings, ropes, pulleys or any device of this type then we consider each body and determine the equation of motion, taking into account all the forces acting upon it. We then equate this to the net force on the body which is given by a formula from Newton's Second Law of motion. The formula is as follows:
a=MtotalFext -----(1)
The net force is nothing but the total mass of the system times the acceleration on the body and this is equated to the total external forces acting on the body which is determined through the free body diagram. One more important point to note is that in these two diagrams a pulley is used to connect the two boxes of varying masses and the friction of the pulley is considered to be negligible and hence the tension in the strings of the pulley is also taken to be neglected as given in the question.
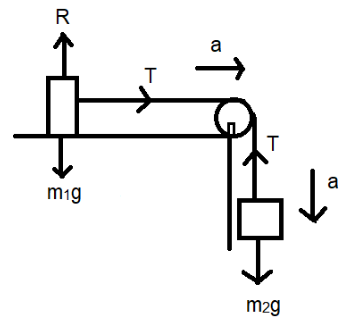
(a) Here we can see that the two connected bodies are attached by a frictionless pulley where one is stationary on a smooth table and another is in motion. The frictional force of the table will not be taken into consideration here because the table is said to be smooth as per the data given in the question.
From the diagram given in the question, we can see that the motion since the 4kg body is hung from the pulley will be in the downward direction and this makes the motion of the 5kg body to move horizontally with it since both are connected. Now, we construct the free body diagram for both of these blocks to see which forces are exerted on them.
From the above diagram, we can see that there are two forces applied on the 5kg body. One is the normal force which is upward due to the table it is placed on and one is gravitational force acting downwards. There is only one force acting on the 4kg block which is the gravitational force acting downwards. The forces acting on the 5kg body get cancelled out as they are in opposite directions to each other. Hence the total force of the system is only the gravitational force acting on the 4kg body and hence the acceleration is downwards. Therefore:
Fext=m2g -----(2)
The tensions of both the strings are not taken into consideration here because both these bodies are connected from the same string of a pulley and hence the tension is the same and it gets cancelled out (since it is in opposite directions).
This force is equated to the net force in accordance with Newton's Second law. We get:
From equation (1)
a=MtotalFext
Here Mtotal is the total mass of the system. Hence:
a=m1+m2Fext
⇒(m1+m2)a=Fext
Since Fext is the total external force on the blocks of the system we can replace Fext. From equation (2) we get:
⇒(m1+m2)a=m2g
Hence the acceleration of the body is given by the equation:
a=m1+m2m2g -----(3)
The acceleration due to gravity, g, value is a constant value given to be 9.8m/s2. But we need the answer in terms of the variable g. Hence we substitute all the given data in the equation (3). We get:
a=5+44g
∴a=94g
Hence, the acceleration of the 5kg body in case (a) is 94g.
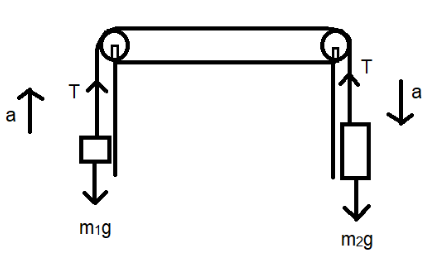
(b) The two blocks are connected by a single string of a pulley and hence the motion will be in the direction of the body with the greater mass which in this case is the 5kg body and hence the acceleration will also be in the downward direction of the 5kg body and correspondingly the 4kg body will accelerate upwards. Now, let us determine the forces exerted on the two blocks using the free body diagram neglecting the tension in the strings of the pulley. We apply the same approach as that of case a).
We can see that there is only one force acting on the two blocks that is the gravitational force. However the gravitational force on the 4kg body opposes the direction of acceleration. Here we apply the concept that forces in the direction of motion is considered positive and forces opposing the direction of motion is considered negative
Hence the total external force of the two blocks in the system will be:
Fext=m1g−m2g-----(4)
Now we apply the equation (1) again:
a=MtotalFext
The total mass, Mtotal , in this system is the sum of the mass of the two blocks. Hence the equation becomes:
a=m1+m2Fext
We now substitute the value from equation (4) into the above equation to get:
a=m1+m2m1g−m2g
We take the common terms out getting:
a=m1+m2(m1−m2)g----(5)
Hence we substitute all the given data in the equation (5). We get:
a=5+4(5−4)g
∴a=91g
Hence, the acceleration of the 5kg body in case (b) is 91g.
Hence the correct option is option B.
Additional information: Newton’s Second Law states that the rate of change of momentum is directly proportional to the external force applied on the body and the change takes place in the direction of the applied force. Newton’s third law is applied in the case of the apparent weight of a man in a lift. A man standing in a lift going downwards with high acceleration tends to feel weightless because the elevator will apply some amount of resistance or force upwards which is said to be the apparent weight of a man in a lift.
Note: The acceleration due to gravity, g, is different from acceleration, a, which may be a common misconception. The g value is a constant value that refers to the acceleration or the corresponding force of the body due to the gravitational pull from the ground while the acceleration of a body may be unique for each body on which varied forces are exerted and due to those external forces the body may accelerate and this acceleration of the body may vary from object to object and may depend on factors like the mass of the object.
