Solveeit Logo
Login

Question

Question: Two bodies of masses 4 kg and 9 kg are separated by distance of 60 cm. A 1 kg mass is placed in betw...

Two bodies of masses 4 kg and 9 kg are separated by distance of 60 cm. A 1 kg mass is placed in between these two masses. If the net force on 1 kg is zero, then its distance from 4 kg mass is
A: 26cm
B: 30cm
C: 28cm
D: 32 cm
E: 24cm

Explanation

Solution

We know that every particle attracts another particle that is kept at a distance, by the law of gravitation. We have to place the 1kg body somewhere in between the other two bodies, else both the bodies will exert an attractive force on the 1kg body in the same direction and the value of the net force on it will not be zero.
Formula used:
Law of gravitation:
F=GMmr2F=\dfrac{GMm}{{{r}^{2}}}, where F is the gravitational force, G is the gravitational constant, M and m are the masses of two bodies and r is the distance between them.

Complete step by step answer:

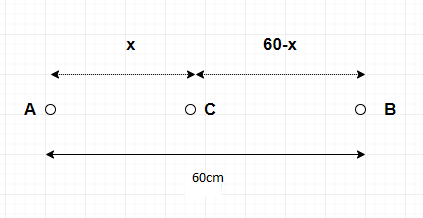
Let the 4kg masses body be A, 9 kg masses body be B and the 1kg massed body be C
Let us assume that the 1kg body is kept at a distance of xxcm from the 4kg mass.
Hence, its distance from the 9kg mass would be 60−x60-xcm.
Let force due to A on C be F⃗AC{{\vec{F}}_{AC}}
From the law of gravitation,
F⃗AC=GmAmCr2=G×4×1x2{{\vec{F}}_{AC}}=\dfrac{G{{m}_{A}}{{m}_{C}}}{{{r}^{2}}}=\dfrac{G\times 4\times 1}{{{x}^{2}}}
Let force due to B on C be F⃗BC{{\vec{F}}_{BC}}
Hence, F⃗BC=GmBmCr2=G×9×1(60−x)2{{\vec{F}}_{BC}}=\dfrac{G{{m}_{B}}{{m}_{C}}}{{{r}^{2}}}=\dfrac{G\times 9\times 1}{{{(60-x)}^{2}}}
We know that the net force on C is zero. Hence the sum of all the forces on C should be zero,
Since the forces F⃗AC{{\vec{F}}_{AC}}and F⃗BC{{\vec{F}}_{BC}}act in opposite directions, we can say that
{{{\vec{F}}}_{AC}}-{{{\vec{F}}}_{BC}}=0 \\\
⇒F⃗AC=F⃗BC \Rightarrow {{{\vec{F}}}_{AC}}={{{\vec{F}}}_{BC}} \\\
⇒4Gx2=9G(60−x)2 \Rightarrow \dfrac{4G}{{{x}^{2}}}=\dfrac{9G}{{{(60-x)}^{2}}} \\\
\Rightarrow 4{{(60-x)}^{2}}=9{{x}^{2}} \\\
Taking square on both sides,
2(60-x)=3x \\\
⇒120−2x=3x \Rightarrow 120-2x=3x \\\
⇒5x=120 \Rightarrow 5x=120 \\\
∴x=1205=24cm \therefore x=\dfrac{120}{5}=24cm \\\
Hence, C is to be kept at a distance of 24cm from A to retain net force as zero.

So, the correct answer is “Option A”.

Note:
Gravitational force is a universal attractive force which obeys the inverse square law.
However it is considered to be the weakest force in nature in case of atomic and subatomic levels.