Question

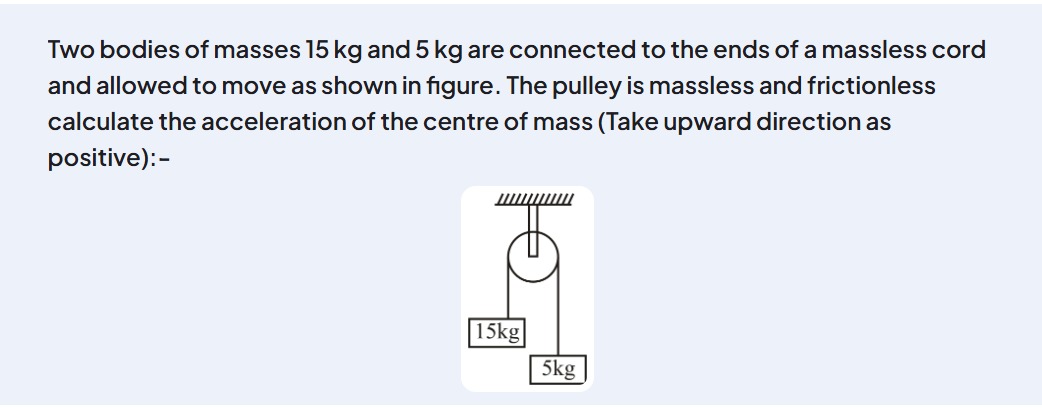
Two bodies of masses 15 kg and 5 kg are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is massless and frictionless calculate the acceleration of the centre of mass (Take upward direction as positive):-

Answer 1

-g/4

Answer 2

The problem describes an Atwood machine setup with two masses connected by a massless cord over a massless, frictionless pulley. We need to find the acceleration of the center of mass of this system, taking the upward direction as positive.

1. Define Masses and Accelerations: Let the two masses be $m_1 = 15$ kg and $m_2 = 5$ kg. Since $m_1 > m_2$, the 15 kg mass will accelerate downwards, and the 5 kg mass will accelerate upwards. Let $a$ be the magnitude of the acceleration of each mass. The acceleration of $m_1$ (15 kg) is $\vec{a}_1 = -a \hat{j}$ (downwards, as upward is positive). The acceleration of $m_2$ (5 kg) is $\vec{a}_2 = +a \hat{j}$ (upwards, as upward is positive).

2. Calculate the Magnitude of Acceleration ($a$): We apply Newton's second law to each mass. Let $T$ be the tension in the cord.

For $m_1 = 15$ kg (moving downwards): The net force is $m_1 g - T$. $m_1 g - T = m_1 a$ $15g - T = 15a$ (Equation 1)

For $m_2 = 5$ kg (moving upwards): The net force is $T - m_2 g$. $T - m_2 g = m_2 a$ $T - 5g = 5a$ (Equation 2)

Add Equation 1 and Equation 2 to eliminate $T$: $(15g - T) + (T - 5g) = 15a + 5a$ $10g = 20a$ $a = \frac{10g}{20} = \frac{g}{2}$

3. Calculate the Acceleration of the Center of Mass ($\vec{a}_{CM}$): The formula for the acceleration of the center of mass for a system of two particles is: $\vec{a}_{CM} = \frac{m_1 \vec{a}_1 + m_2 \vec{a}_2}{m_1 + m_2}$ Substitute the values of masses and their accelerations: $\vec{a}_{CM} = \frac{(15 \text{ kg}) \left(-\frac{g}{2} \hat{j}\right) + (5 \text{ kg}) \left(+\frac{g}{2} \hat{j}\right)}{15 \text{ kg} + 5 \text{ kg}}$ $\vec{a}_{CM} = \frac{-\frac{15g}{2} \hat{j} + \frac{5g}{2} \hat{j}}{20}$ $\vec{a}_{CM} = \frac{\left(\frac{-15g + 5g}{2}\right) \hat{j}}{20}$ $\vec{a}_{CM} = \frac{\left(\frac{-10g}{2}\right) \hat{j}}{20}$ $\vec{a}_{CM} = \frac{-5g \hat{j}}{20}$ $\vec{a}_{CM} = -\frac{g}{4} \hat{j}$ The negative sign indicates that the acceleration of the center of mass is in the downward direction.

If we take the standard value of $g = 10 \text{ m/s}^2$: $\vec{a}_{CM} = -\frac{10}{4} \hat{j} = -2.5 \hat{j} \text{ m/s}^2$