Question
Question: Two bodies of mass 4 and 6 kg are attached to the ends of a string passing over a pulley. The 4 kg m...
Two bodies of mass 4 and 6 kg are attached to the ends of a string passing over a pulley. The 4 kg mass is attached to the table top by another string. The tension in this string T1 is equal to
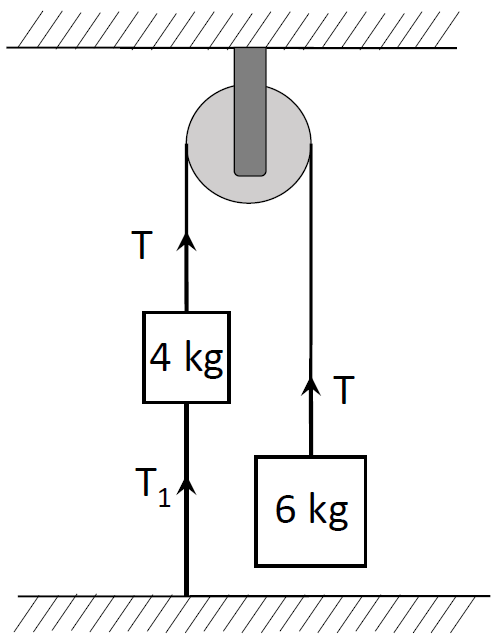
Solution
Hint: All the bodies are in a state of rest and the net force acting on each of them is zero. First find value of T using force balance on 6 kg body and considering frictionless pulley use this value to find T1 by considering force balance on 4 kg body.
Complete answer:
In the above system, all the bodies are in a state of rest. So there is no net acceleration on anybody and thus no net force is acting on both the masses. Let the tension in the string connecting both the masses be T. This tension will be an upward force acting on mass 6kg. If we consider the 6 kg mass then we have two forces acting on it. Tension, T is balancing the weight of the mass in downward direction. Both these forces are in the opposite direction. Let the acceleration due to the gravity be g=9.8m/s2. Therefore,
T=mg where m=6kg.
T=6×9.8=58.8N
They have not specified any details about pulley, so we will assume it is frictionless and then consider that this tension remains same over it and acts on 4kg mass in the upward direction balancing the tension in the bottom string which connects the 4kg mass to the table and the weight of the mass. Therefore, we can write the force balance for 4kg mass as follows:
T1+m1g=T=58.8N, where m1=4kg
⇒T1=58.8−4×9.8 ⇒T1=19.6N
Note: Many times, acceleration due to gravity is considered 10m/s2 for its simplicity in calculations. So better to carry the term till the end and substitute accordingly if the numerical value is required in multiple choice questions.
