Question

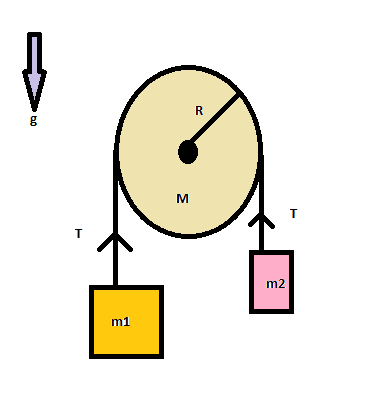
Two bodies ${m_1}$ and ${m_2}$are attached to the two ends of a string figure. The string passes over a pulley of mass $M$ and radius $R$. If ${m_1} > {m_2}$, then the acceleration of the system is
(A) $\dfrac{{({m_1} - {m_2} + M)g}}{{{m_1} + {m_2} + M}}$
(B) $\dfrac{{({m_1} - {m_2})g}}{{{m_1} + {m_2}}}$
(C) $\dfrac{{({m_1} + {m_2})g}}{{{m_1} - {m_2}}}$
(D) $\dfrac{{({m_1} - {m_2})g}}{{{m_1} - {m_2} - M/2}}$

Answer 1

Hint Since it is given in the question that ${m_1} > {m_2}$, the system of the two bodies connected by the string (assumed massless) will have a net acceleration such that ${m_2}$ rises upwards. We can balance forces on the two blocks separately such that they have the same acceleration with opposite signs. This is because if they have different accelerations, then either the string will slacken or tear apart which is not allowed.

Complete Step by step solution We assume that the tension in the string is $T$. This tension is the same at all places in the same string with proper directions. Also we have to assume that the heavier block ${m_1}$ is moving downwards with an acceleration $a$.

Now using Newton’s ${2^{nd}}$ Law on ${m_2}$, we get
$T - {m_2}g = {m_2}a$, since ${m_2}$ is going up with acceleration $a$ (i)
Again using Newton’s ${2^{nd}}$ Law on ${m_1}$, we get
${m_1}g - T = {m_1}a$, since ${m_1}$ is going down with acceleration $a$ (ii)
Eliminating $T$ from the above equations (i) & (ii), we get
${m_1}g - {m_2}g - {m_2}a = {m_1}a$, such that we get
$a = \dfrac{{({m_1} - {m_2})g}}{{{m_1} + {m_2}}}$.

$\therefore$ Option $(B)$ is correct.

Note The tension $T$ in the same string is always uniform everywhere on the same string at an instant of time and the string has an acceleration $a$ everywhere. We will assume all strings to be massless. We will also have to assume that the center of the pulley is hinged at some point otherwise the entire system, i.e. the blocks and the pulley will have an acceleration of $g = 9.80432\,m/{s^2}$, i.e. they will fall freely under gravitational attraction. The string should be assumed massless so that the tension is uniform in the string, otherwise tension in the string will vary since the mass of the string at different points will add to the net mass being supported by the string at different points.