Question

Two bodies are projected with the same velocity. One body is projected at an angle of $30^{\circ}$ and the other at an angle of $60^{\circ}$ to the horizontal. The ratio of the maximum heights reached is
A. $3:1$
B. $1:3$
C. $1:2$
D. $2:1$

Answer 1

A body when projected at an inclination from the ground, it is said to experience projectile motion. Then the path followed by the body is called the ballistic trajectory, which is a curved parabolic path. Here, we have to find the ratio between the maximum heights, when the angle of inclination is varied.

Formula used:
$H=\dfrac{u^2sin^2\theta}{2g}$

Complete step by step answer:
Let $u$ be the initial velocity of the body which is projected at an angle $\theta$ from the horizontal. Then the initial velocity $u$ can be resolved into two components along the x and y axis respectively .Let $H$ and $R$ be the maximum distances along the x and y-axis respectively, during the time of flight $T$.Consider the figure as shown below:

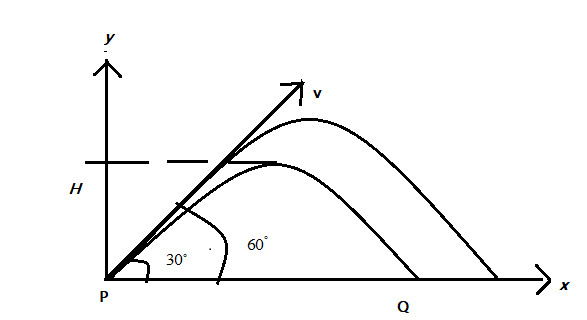
We know from projectile motion that the maximum height $H$ attained by an object which is inclined by some angle $\theta$ is given as $H=\dfrac{u^2sin^2\theta}{2g}$
Here, we have two angles, $\theta_1=30^{\circ}$ and $\theta_2=60^{\circ}$. Let, $H_1$ be the height due to $\theta_1$ and $H_2$ be the height due to $\theta_2$, then taking the ratio of the heights we have,
$\dfrac{H_1}{H_2}=\dfrac{\left(\dfrac{u^2sin^230}{2g}\right)}{\left(\dfrac{u^2sin^260}{2g}\right)}$
Since both the inclination have the same initial velocity, we get
$\implies \dfrac{H_1}{H_2}=\dfrac{sin^230}{sin^260}$
$\implies \dfrac{H_1}{H_2}=\dfrac{\left(\dfrac{1}{2}\right)^2}{\left(\sqrt{\dfrac{3}{2}}\right)^2}$
$\implies \dfrac{H_1}{H_2}=\dfrac{1}{3}$

So, the correct answer is “Option B”.

Note: When the object is on the air, the only force acting on the body is the force due to gravitation, which pulls the object back to the surface at the speed of acceleration due to gravity. Note that the height of the projected body doesn’t depend on the mass of the body. Here, however we are using the equation of trajectory of the projectile to solve the problem.