Question

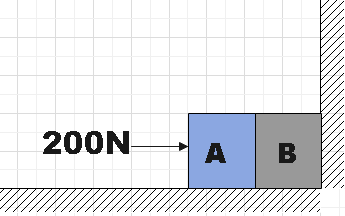
Two bodies A and B of mass 5kg and 10kg in contact with each other rest on a table against a rigid wall. The coefficient of friction between the bodies and the table is 0.2. When the force of 200N is applied horizontally on A, which of the following is correct? $\left( g=10m{{s}^{-2}} \right)$
A. The reaction of the wall is 200N
B. The action reaction force between A and B is more than the reaction of the wall.
C. The action reaction force between A and B is less than the reaction of the wall.
D. Both A and C are correct.

Answer 1

You could get the reaction of the wall on the system as the result of the applied horizontal force from the difference of that force and the frictional force on the system. Similarly you could find the force exerted by A on B from the difference of the applied force and frictional force on A. Then you could compare the two forces obtained and thus answer the question.
Formula used:
Frictional force,
$f=\mu N$

Complete answer:
We are given:
${{m}_{A}}=5kg$
${{m}_{b}}=10kg$
${{\mu }_{s}}=0.15$
$F=200N$

(a) The frictional force on the system would be given by,
$f=\mu N=\mu \left( {{m}_{A}}+{{m}_{B}} \right)g$
$\Rightarrow f=0.15\left( 5+15 \right)9.8$
$\therefore f=22.05N$
The net force on the partition can be given by,
${{F}_{net}}=F-f$
$\Rightarrow {{F}_{net}}=200-22.05$
$\therefore {{F}_{net}}=177.95N$ (To the right)
From the third law of motion we know that the reaction force on the partition will be in the opposite direction to the net force on the partition. So the reaction will be 177.95N (To the left).

(b) Let us take ${{f}_{a}}$ and ${{f}_{b}}$ to be the frictional forces on the bodies A and B respectively.
${{f}_{A}}=\mu {{N}_{A}}=\mu {{m}_{A}}g$
$\Rightarrow {{f}_{A}}=0.15\times 5\times 9.8$
${{f}_{A}}=7.35N$
The force on body B exerted by A will be the difference of the applied horizontal force and the frictional force on A. That is,
${{F}_{B}}=F-{{f}_{A}}$
$\Rightarrow {{F}_{B}}=200-7.35$
$\therefore {{F}_{B}}=192.65N$ (Towards right)
Now the normal reaction on body A exerted by B will have the same magnitude and opposite direction (Towards left).
${{F}_{A}}=-192.65N$
Therefore, we could conclude that the action reaction force between A and B is more than the reaction of the wall.

Hence, option B is found to be the correct statement.

Note:
The frictional force is known to be a limiting force because it’s very definition says that it opposes the relative motion between two bodies. So whenever there is a relative motion between two surfaces the frictional force comes into picture, until and unless it is mentioned that the surfaces are smooth.