Question

Two bodies A and B of mass $5kg$ and $10kg$, in contact with each other rest on a table against a rigid wall (see figure). The coefficient of friction between the bodies and the table is $0.2$. A force of $200N$ is applied horizontally to A. What are
(a) the reaction of the vertical wall.
(b) the action-reaction forces between A and B?
(c) What happens when the wall is removed? Does the answer to (b) change, when the bodies are in motion?
Ignore the difference between ${{\mu }_{s}}$ and ${{\mu }_{k}}$

Answer 1

Mass of the two bodies, force acting and coefficient of friction are given in the question. Here, the external force is applied on A due to which the wall is exerting a reaction force. By drawing the free body diagram, we will get an idea about the forces and reaction forces acting on the blocks individually and together as a system. Then, by using formula for friction, normal force, Newton’s second law we can solve this question.
Formula used:
${{F}_{friction}}=\mu N$
$N=mg$
$a=\dfrac{F}{m}$

Complete answer:

Given,
Mass of A,${{m}_{1}}=5kg$
Mass of B,${{m}_{2}}=10kg$
External force,$F=200N$
Coefficient of friction, $\mu =0.2$
a) Let’s draw the free body diagram of both A and B.

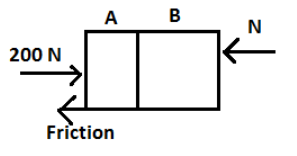
The forces acting on the system are,
External force $200N$, reaction force exerted by the wall $R$ and frictional force between ground and body ${{F}_{friction}}$.
Then,
Reaction force, $R=200-{{F}_{friction}}$ ------------- 1
We have,
${{F}_{friction}}=\mu N$ ---------------- 2
Where,
$\mu$ is the coefficient of friction
$N$is the normal force acting on the entire system
We have,
$N=mg$
Where,
$m$is the mass of the body
Here, $m={{m}_{1}}+{{m}_{2}}$
$g$is the acceleration due to gravity
Then,
$N=\left( {{m}_{1}}+{{m}_{2}} \right)g$
Substitute the values of ${{m}_{1}}$, ${{m}_{2}}$ and $g$in the above equation we get,
$N=\left( 5+10 \right)\times 10=150N$
Substitute the above value of $N$ and $\mu$ in equation 2, we get,
${{F}_{friction}}=0.2\times 150=30N$
Then,
$R=200-30=170N$
the reaction of the vertical wall is $170N$.

b)

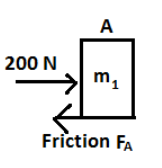
Free body diagram of A.
Forces acting on body A are, external force $200N$, and frictional force ${{F}_{A}}$
Then,
Frictional force, ${{F}_{A}}=\mu {{m}_{1}}g$
Substitute the values of ${{m}_{1}}$, $\mu$ and $g$in the above equation, we get,
${{F}_{A}}=0.2\times 5\times 10=10N$
Then, the net force acting on B due to A is,
$F'=200-10=190N$
Therefore, force acting on A due to B is $190N$.

c) When the wall is removed, both the bodies start moving. Then,
Acceleration of the system, $a=\dfrac{F}{{{m}_{1}}+{{m}_{2}}}$
Here, the net force acting on the system will be, $F''=200-30=170N$
Then,
Acceleration of the system, $a=\dfrac{170}{5+10}=11.33m/{{s}^{2}}$
Then, the force which moves block A is, $F'''={{m}_{1}}a=5\times 11.33=56.65N$
But, the force acting on A due to B is $190N$
Then, the net action force on A $=190-56.65=133.35N$
Therefore, force acting on B due to A $=133.35N$
Hence, when the wall is removed, the action and reaction forces on A and B will also change.

Note:
Friction is of two types: static friction and kinetic friction. Static friction is applied on the body at rest, or the body which is about to move. Static friction opposes the movement of the body. Its value is equal to applied force till the body remains in static position. i.e., it self-adjusts its value according to applied force.