Question

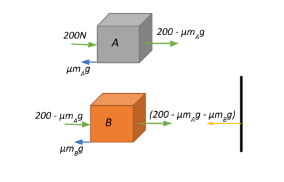
Two bodies A and B of mass $5\;kg$ and $10\;kg$, in contact with each other rest on a table against a rigid wall (see figure). The coefficient of friction between the bodies and the table is $0.15$. A force of $200\;N$ is applied horizontally to A. What are (a) the reactions of the vertical wall? (b) the action-reaction forces between A and B? What happens when the wall is removed? (c) Does the answer to (b) change when the bodies are in motion? Ignore the difference between $\mu_s$ and $\mu_k$.

Answer 1

For part (a) Calculate the amount of applied force that is spent to overcome friction by both bodies, and the resultant force will be equivalent to the reaction of the vertical wall, (b) Similar to part (a) except you calculate the amount of force spent on friction by A and B separately and remember that every action produces an equal and opposite reaction, and (c) If the bodies are in motion, remember that force due to acceleration becomes a contributing factor in addition to frictional and applied forces. Account for this force due to acceleration as well while calculating your net force.

Formula used:
Force $F_{applied} = mg$, where m is the mass of the body and g is the acceleration due to gravity.
Frictional force $F_{frictional} = \mu mg$ where $\mu$ is the coefficient of friction.

Complete answer:
Let us deconstruct the question to gain an understanding.

From the figure, we see that we have two bodies in contact with each and a force of $200\;N$ is applied horizontally on A. This force gets transferred to the rigid wall via B and the wall produces a reaction force in a direction opposite to the applied force. However, the interaction between A and B, and B and the wall, will be by overcoming friction between the bodies and the table, and a certain amount of the incident force is spent in overcoming these regions of friction, i.e.,
$F_{frictional} = \mu m_A g +\mu m_B g = \mu \left(m_A +m_B\right) g$
$\Rightarrow F_{frictional} = 0.15 \times \left(5 + 10\right)\times 9.8 = 22.05\;N$ directed leftwards.

a.)Now, from Newton’s third law of motion we have that for every action, there is an equal and opposite reaction. Therefore, the net force that reaches the vertical wall will also be the normal reaction produced by the vertical wall, given by
$N_{vertical\;wall} = F_{applied} – F_{frictional} = 200 – 22.05 = 177.95\;N$ directed leftwards.

b.)Now, let us analyse the action-reaction forces between A and B.
To transmit the applied force of $200\;N$ to B, A has to overcome a frictional force of :
$F_{frictional} = \mu m_A g = 0.15 \times 5 \times 9.8 = 7.35\;N$ directed leftward.
This gets spent from the applied force and the force applied by body A on body B will be $F_{A \rightarrow B}= 200 -7.35 = 192.65\;N$ directed rightwards and body B exerts a normal reaction force on body A of the same magnitude but in the opposite direction.

Now body B transmits this force to the wall but it has to overcome a friction of
$F_{frictional} = 0.15 \times 10 \times 9.8 = 14.7\;N$ directed leftwards. Therefore, body B applies a force of $F_{net} = 192.65 – 14.7 = 177.95\;N$ directed rightwards.
If the wall is removed, the two bodies will move in the direction of the applied force and the net force acting on the moving system will be $F_{net}=177.95\;N$

c.)We now have to deduce if the force exerted by A on B will change if the bodies are in motion.
The equation of motion for this system of two bodies in acceleration can be written as:
$F_{net} = \left(m_A +m_B\right)a$ where a is the acceleration of the system.
$\Rightarrow a = \dfrac{F_{net}}{\left(m_A +m_B\right)} = \dfrac{177.95}{5+10} = 11.86\;ms^{-2}$

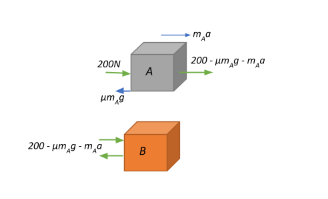
Thus, the force that contributes to the motion of A can be calculated:
$F_{A} = m_A a = 5 \times 11.86 = 59.32\;N$
This force gets spent from the force transmitted from A to B.
Therefore, the net force exerted by A on B will now be: $F_{A \rightarrow B}- F_{A} = 192.65 – 59.32 = 133.33\;N$ and B exerts a normal reaction force on A of the same magnitude but in the opposite direction.

Note:
Remember to account for attenuation of the applied force due to friction and also due to acceleration. Overlooking these parameters will produce inconsistent results.
Also, notice that there is always a reaction produced from every component of the system when a force is applied. The best way to remember this is to just apply newton’s third law of motion in its most bare form.
And do not forget that friction and normal reaction are always in a direction opposite to the applied force, so calculate the net force at each point accordingly.