Question

Two bodies $3\,Kg{\kern 1pt} {\kern 1pt} and{\kern 1pt} {\kern 1pt} 4Kg$ are suspended at the ends of a massless string passing over a frictionless pulley. The acceleration of the system is $(g = 9.8\,m{s^{ - 2}})$
A. $4.9\,m{s^{ - 2}}$
B. $2.45\,m{s^{ - 2}}$
C. $1.4\,m{s^{ - 2}}$
D. $9.5\,m{s^{ - 2}}$

Answer 1

In order to solve this question, we will first draw the appropriate diagram according to the given information and then will balance the all forces acting on each black and since four Kilogram block will have more weight so it move downward whereas three kilogram block will move upward through the pulley and then we will find the value of acceleration of the system.

Complete step by step answer:
Let us suppose a be the acceleration of the system and T be the tension acting on the string and weight of each body acting in downward direction and the direction of each forces acting on the bodies are shown in the diagram as,

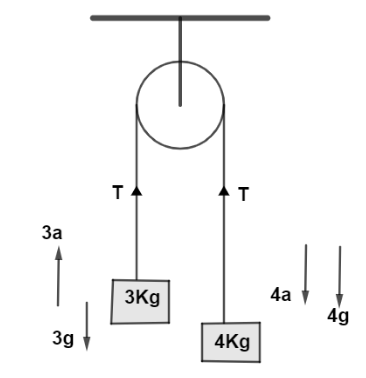
Now, for body of mass $3kg$ we have forces direction as in diagram so, balancing the forces we have,
$3a = T - 3g$ where g is the acceleration due to gravity so,
$\Rightarrow 3a = T - 3g \to (i)$
Now, for body of mass $4\,kg$ we have forces direction as in diagram so, balancing the forces we have,
$4a = 4g - T \to (ii)$
Now, add the both equations (i) and (ii) we get,
$4a + 3a = 4g - 3g + T - T$
$\Rightarrow 7a = g$
according to the problem we have given that $(g = 9.8m{s^{ - 2}})$ so,
$a = \dfrac{{9.8}}{7}$
$\therefore a = 1.4\,m{s^{ - 2}}$

Hence, the correct option is C.

Note: It should be remembered that the tension is the force acting on the string when it moves and since the string is massless and pulley is frictionless so the acceleration of each body is the same and that acceleration is the acceleration of the whole system. All the forces whether its tension force or weight all have the same units Newton.