Question

Two boats approach the lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are $30^\circ$ and $45^\circ$. If the distance between the two boats is 100 m, find the height of the lighthouse.

Answer 1

Here, we will first draw the triangle using the given condition to simplify the calculation. Then we will use the tangential property, that is, $\tan {\text{A}} = \dfrac{p}{b}$, where $p$ is the perpendicular and $b$ is the base in triangle with angles 30 degrees and 45 degrees, separately to find the value of CA and DA. Then we will substitute the value back to find the height of the lighthouse.

Complete step by step answer:
We are given that two boats approach the lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are $30^\circ$ and $45^\circ$. The distance between the two boats is 100 m.
Let us assume that BA represents the height of the lighthouse, the position of the first boat is at C and the second boat is at D.
First, we will draw the triangle using the given conditions.

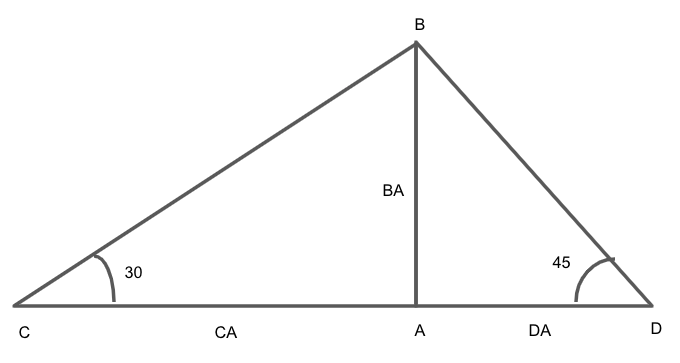
Since we know that from the diagram, the point C, D and A lies on the same line segment and the distance between two boats CD is 100 m. Then, we have

$$\Rightarrow CD = CA + DA \\\ \Rightarrow 100 = CA + DA \\\ \Rightarrow CA + DA = 100{\text{ ......eq.(1)}} \\\$$

We will first take the triangle $\Delta DAB$, where $\angle DAB = 90^\circ$.
We will use the tangential property, that is, $\tan {\text{A}} = \dfrac{p}{b}$, where $p$ is the perpendicular and $b$ is the base.
Using the above tangential property, we get
$\tan 45^\circ = \dfrac{{BA}}{{DA}}$
Substituting the values of $\tan 45^\circ = 1$ in the above equation, we get
$\Rightarrow 1 = \dfrac{{BA}}{{DA}}$
Cross-multiplying the above equation, we get
$DA = BA{\text{ ......eq.}}\left( 2 \right)$
We will now take the triangle $\Delta DAB$, where $\angle CAB = 90^\circ$.
We will use the tangential property, that is, $\tan {\text{A}} = \dfrac{p}{b}$, where $p$ is the perpendicular and $b$ is the base.
Using the above tangential property, we get
$\tan 30^\circ = \dfrac{{BA}}{{CA}}$
Substituting the values of $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ in the above equation, we get
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{BA}}{{CA}}$
Cross-multiplying the above equation, we get
$CA = BA\sqrt 3 {\text{ ......eq.}}\left( 3 \right)$
Using the equation (2) and equation (3) in equation (1), we get

$$\Rightarrow BA\sqrt 3 + BA = 100 \\\ \Rightarrow BA\left( {\sqrt 3 + 1} \right) = 100 \\\$$

Multiplying the above equation by $\sqrt 3 - 1$ on both sides, we get
$\Rightarrow BA\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 - 1} \right) = 100\left( {\sqrt 3 - 1} \right)$
Using the rule, $\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}$ in the above equation, we get

$$\Rightarrow BA\left( {{{\left( {\sqrt 3 } \right)}^2} - {1^2}} \right) = 100\left( {\sqrt 3 - 1} \right) \\\ \Rightarrow BA\left( {3 - 1} \right) = 100\left( {\sqrt 3 - 1} \right) \\\ \Rightarrow 2BA = 100\left( {\sqrt 3 - 1} \right) \\\$$

Dividing the above equation on both sides by 2, we get

$$\Rightarrow \dfrac{{2BA}}{2} = \dfrac{{100\left( {\sqrt 3 - 1} \right)}}{2} \\\ \Rightarrow BA = 50\left( {\sqrt 3 - 1} \right) \\\$$

Therefore, the height of the lighthouse is $50\left( {\sqrt 3 - 1} \right)$ meters.

Note: In solving these types of questions, you should be familiar with the concept of angle of elevation and the tangential properties. Students should make the diagram for better understanding. Using the values of respective angles you can simply find any length present in the figure using the tangential value ‘$\tan$’, which makes our problem easy to solve. We will multiply the root number with itself is equal to the number. For example, the product of$\sqrt 3$ with itself is 3. We can use the cot as well instead of tan.