Question

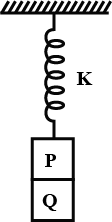
Two blocks $P$ and $Q$ of masses $0.3\,\text{Kg}$ and $0.4\,\text{kg}$ respectively are stuck to each other by some weak glue as shown in the figure. They hang together at the end of a spring with a spring constant $k=240\,\text{nm}$ . If the block Q suddenly falls free due to the failure of glue, find
(i) period of SHM of block P
(ii) The amplitude of its SHM
(iii) The total energy of oscillation of the system.

Answer 1

Hint : Initially when both the blocks are attached and they are hung with the help of spring, assuming they both are in equilibrium, then the force due to gravity must be equal to the restoring force. We can make use of equilibrium conditions to find out the spring constant and other quantities that are the length of the spring. When a body oscillates, then it undergoes simple harmonic motion and its time period is given by: $T=2\pi \sqrt{\dfrac{m}{k}}$ .

Complete Step By Step Answer:
When the two blocks are attached, then the forces in the vertical can be given as:
$k{{x}_{0}}=\left( {{m}_{1}}+{{m}_{2}} \right)g$
Now we substitute the values in given formula,
$\Rightarrow 200{{x}_{0}}=\left( 0.3+0.4 \right)\times 10$
$\Rightarrow 200{{x}_{0}}=7$
$\Rightarrow {{x}_{0}}=\dfrac{7}{200}m$
Now, the block Q is removed and so net force acting is in the upward direction, so block P moves up and undergoes SHM, its time period can be given as:
$\Rightarrow T=2\pi \sqrt{\dfrac{{{m}_{1}}}{k}}$
Now we substitute the values in the above equation as
$T=2\pi \sqrt{\dfrac{0.3}{200}}$
Simplify the above equation as,
$\therefore T=243s$
Now when the block Q is removed, the force in the downward direction decreases and hence spring has the tendency to move up. The spring will move up till the time the restoring force is equal to the weight of the block P.
$\Rightarrow kx={{m}_{p}}g$
$\Rightarrow 200x=0.3\times 10$
$\Rightarrow x=\dfrac{3}{200}m$
(ii) Now we calculate the amplitude of SHM as,
$\Rightarrow \Delta x={{x}_{0}}-x$
$\Rightarrow \Delta x=\dfrac{7}{200}-\dfrac{3}{200}$
After substituting the values, we get,
$\therefore \Delta x=0.02\,\text{m}$
(iii) In an exceedingly very straightforward harmonic generator, the energy oscillates between energy of the mass of kinetic energy and P.E. keep inside the spring. inside the SHM of the mass and spring system, there are no dissipative forces, thus the entire energy is that the entire of the P.E. and energy. Throughout this section, we tend to tend to require into consideration the conservation of energy of the system. The concepts examined are valid for all straightforward harmonic oscillators, alongside those were the gravitation plays employment.
Total energy of oscillation:
$K=\dfrac{1}{2}k{{x}_{0}}^{2}$
Now we substitute the values as,
$\Rightarrow K=\text{1}/\text{2}\times \text{2}00\times {{\left( \text{7}/\text{2}00 \right)}^{2}}$
$\therefore K=0.\text{1225J}$ .

Note :
The angular frequency depends alone on the force constant and conjointly the mass, and not the amplitude. The angular frequency is introduced as, that provides an equation for the quantity of the motion. Also, when a body is in free fall like here the block Q, the body has constant acceleration but not constant velocity. Also, the law of conservation of energy holds until we assume there is no loss of energy due to friction in the form of heat.