Question

Two blocks of masses $M$ and $2M$ are connected to a light spring constant $K$ that has one end fixed, as shown in the figure. The horizontal surface and the pulley are frictionless. The blocks are released from rest when the spring is non-deformed. The string is light.

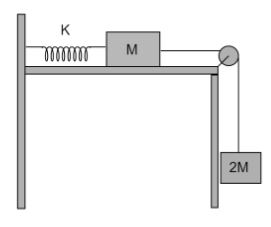
A. Maximum extension in the spring is $\dfrac{{4Mg}}{K}$.
B. Maximum kinetic energy of the system is $\dfrac{{2{M^2}{g^2}}}{K}$.
C. Maximum energy stored in the spring is four times that of the maximum kinetic energy of the system.
D. When the kinetic energy of the system is maximum, Energy stored in the spring is $\dfrac{{4{M^2}{g^2}}}{K}$.

Answer 1

To solve this question, we need to apply the work-energy theorem on the whole system. The blocks are released from rest thus, initial kinetic energy is zero and at the maximum extension of spring, the blocks will be momentarily at rest. Thus, we can apply the work-energy theorem and find out the maximum extension. The system will have maximum kinetic energy when the net force on the system is zero.

Complete step by step answer:
Two blocks of masses $M$ and $2M$ are connected and are released from rest and initially, spring is at its natural length. The stiffness of the spring is $K$. As they are released from rest the initial kinetic energy is zero. At the maximum extension of the spring, the two blocks will be momentarily at rest thus kinetic energy at this point will also be zero.Let the maximum extension of the spring be $x$.

Applying work-energy theorem,
${K_f} - {K_i} = {W_{\text{all forces}}}$
$\Rightarrow {K_f} - {K_i} = {W_{gravity}} + {W_{spring}} + {W_{tension}}$
$\Rightarrow 0 - 0 = 2Mgx + \left( { - \dfrac{1}{2}K{x^2}} \right) + 0$
On solving we get,
$\Rightarrow 2Mgx = \dfrac{1}{2}K{x^2}$
$\Rightarrow x = \dfrac{{4Mg}}{K}$
Hence, the maximum extension in the spring is $\dfrac{{4Mg}}{K}$.

At maximum kinetic energy the net forces on the whole system must be equal to zero. Therefore, all the forces must be balanced
$T = 2Mg$
$\Rightarrow T = Kx = 2Mg$
$\Rightarrow x = \dfrac{{2Mg}}{K}$
Applying work-energy theorem,
$\Rightarrow {K_f} - 0 = 2Mgx + \left( { - \dfrac{1}{2}K{x^2}} \right) + 0$
Substituting the values and solving we get,
${K_f} = \dfrac{{4{M^2}{g^2}}}{K} - \dfrac{{2{M^2}{g^2}}}{K}$
$\Rightarrow {K_f} = \dfrac{{2{M^2}{g^2}}}{K}$
Therefore, maximum kinetic energy is $\dfrac{{2{M^2}{g^2}}}{K}$

Energy stored in the spring is given by $\dfrac{1}{2}K{x^2}$.
Energy stored in the spring at maximum kinetic energy is,
$\dfrac{1}{2}K{\left( {\dfrac{{2Mg}}{K}} \right)^2}$
Energy stored in the spring at maximum kinetic energy is $\dfrac{{2{M^2}{g^2}}}{K}$.
Maximum energy stored in the spring is when there is maximum extension.
Maximum energy stored in spring is $\dfrac{1}{2}K{\left( {\dfrac{{4Mg}}{K}} \right)^2}$
Maximum energy stored in the spring is $\dfrac{{8{M^2}{g^2}}}{K}$ which is four times the maximum kinetic energy of the system.

Hence, options A., B., and C. are the correct options.

Note: The work-energy theorem rule came from Newton's second law, and hence it is applicable to the particles. Objects that are like particles are considered for this rule. So, if all the object particles behave like particles, we can consider the whole object as a particle.