Solveeit Logo
Login

Question

Question: Two blocks of masses \({M_1} = 4kg\) and \({M_2} = 6kg\) are connected by a string of negligible mas...

Two blocks of masses M1=4kg{M_1} = 4kg and M2=6kg{M_2} = 6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1{M_1} and the horizontal surface is 0.4. When the system is released the masses M1{M_1} and M2{M_2} start accelerating. What additional mass mm should be placed over M so that the masses (M1{M_1} + mm) slide with a uniform speed?

(A) 12kgs
(B) 11khs
(C) 10kgs
(D) 9kgs

Explanation

Solution

In this question we are asked to find out the mass of the unknown weight mm such that the masses (M1{M_1} + mm) slide with a uniform speed. Now in case of uniform velocity the net force should be balanced or the sum of the net forces on the masses (M1{M_1} + mm) should be equal to zero.

Complete answer:
Now at first let's draw the free body diagram of the two bodies (M1{M_1} + mm).

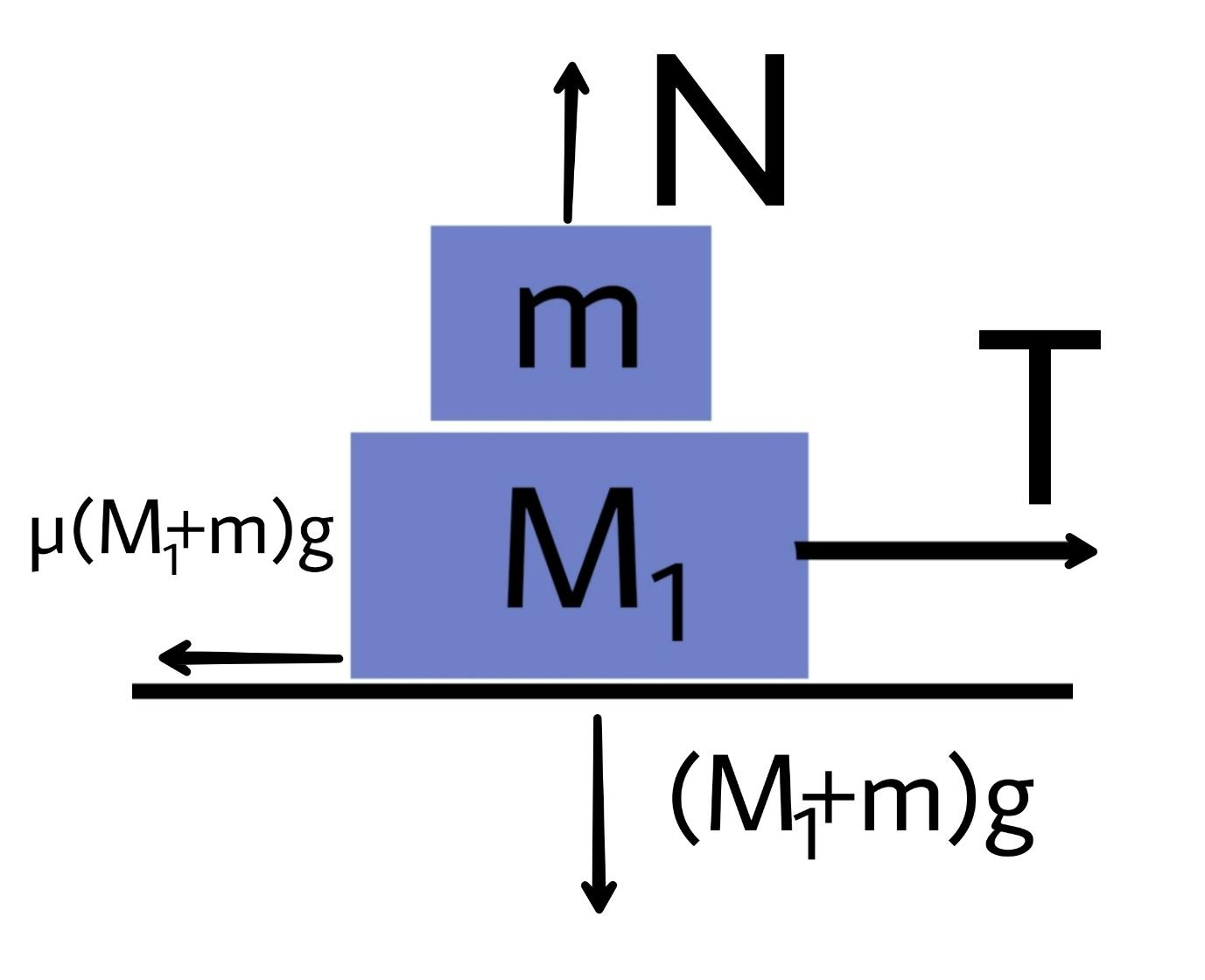
Here the y component of force balances each other so the weight becomes equal to the normal.
(M1+m)g=N\left( {{M_1} + m} \right)g = N
Since the masses move at a uniform speed the tension force balances the friction force.
μ(M1+m)g=T\mu \left( {{M_1} + m} \right)g = T equation 1
Now in this second diagram we analyze the mass.

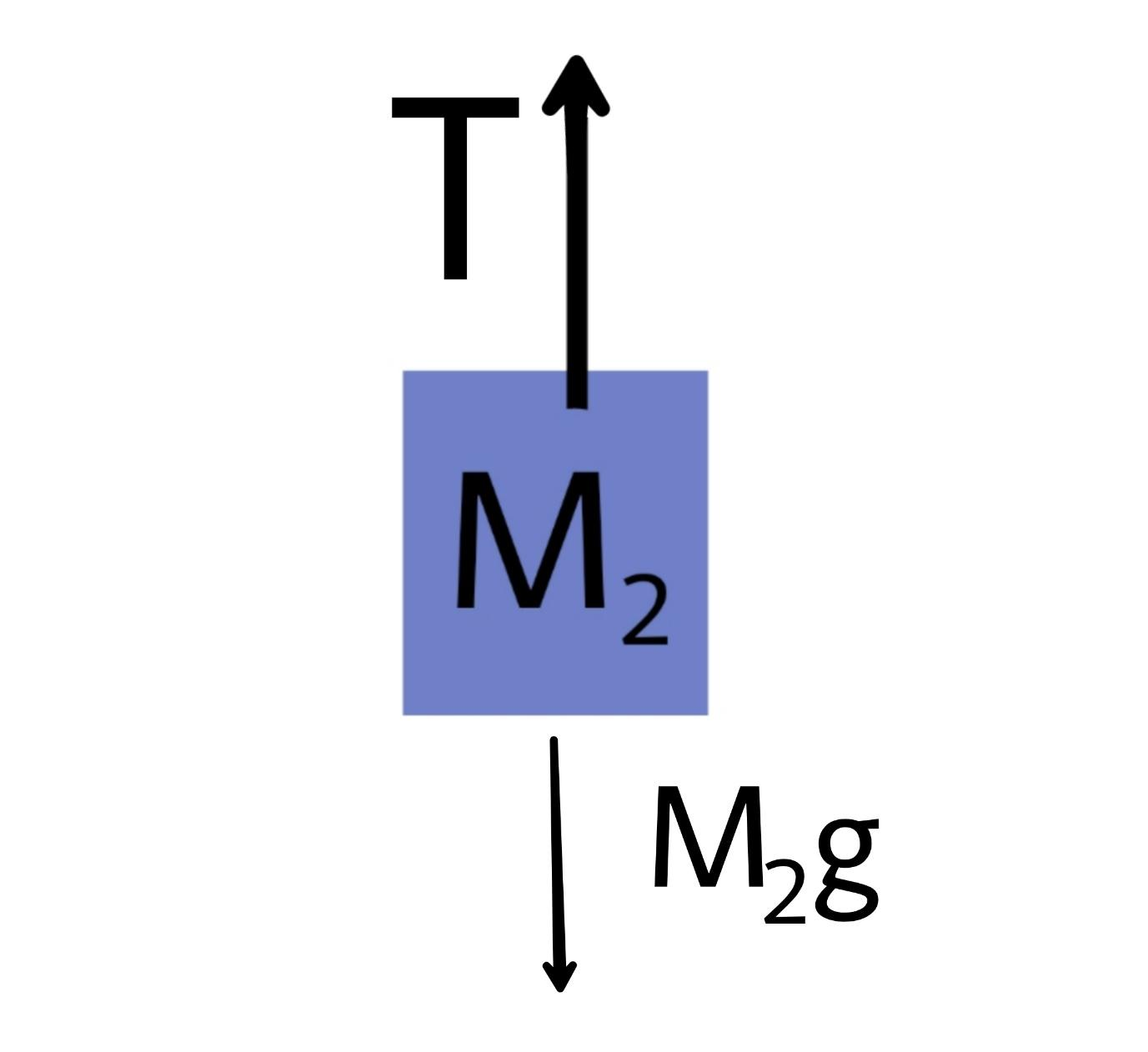
Since the motion is a uniform speed motion the net force on M2{M_2} becomes zero so the tension force balances the weight of M2{M_2}
T=M2gT = {M_2}g equation 2
Thus, from equation 1 and 2 we get
μ(M1+m)g=M2g\mu \left( {{M_1} + m} \right)g = {M_2}g
μ(M1+m)=M2\mu \left( {{M_1} + m} \right) = {M_2}
m=M2μ−M1m = \dfrac{{{M_2}}}{\mu } - {M_1}
Now let’s substitute the values.
m=60.4−4=15−4=11kgsm = \dfrac{6}{{0.4}} - 4 = 15 - 4 = 11kgs
So, the mass of the unknown object is m = 11kgs

The correct option is (B).

Note:
In every case of whether the object is at rest or it is in motion the net force that is acting on the object should be equal to zero, we can also See this from Newton's second law of motion. Here in this question the friction between the ropes and the pulley is ignored. But if there was friction present in the pulley then the rotational motion of the pulley was also to be considered in solving the problem.