Question
Question: Two blocks of masses \({m_1} = 1.5kg\) and \({m_2} = 2kg\) are attached to each other by strings and...
Two blocks of masses m1=1.5kg and m2=2kg are attached to each other by strings and pulleys as shown in figure. Assume that pulleys are massless and frictionless and strings are massless. The system is released. If the table is frictionless, find the acceleration of m1 and m2. Take g=10ms−2
A. 5ms−2and 2.5ms−2
B. 10ms−2 and 5ms−2
C. 15ms−2 and 7.5ms−2
D. 20ms−2 and 10ms−2
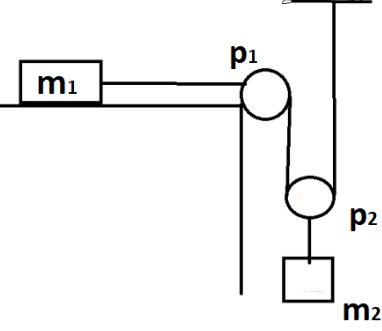
Solution
To find the acceleration along the two masses we have to find the motion in which the respective masses are moving after that we can apply the formula for tension. Tension is defined as the product of masses and the gravitational force (g) subtracting the acceleration. After getting the equation of tension we can simply find the acceleration.
Complete step by step answer:
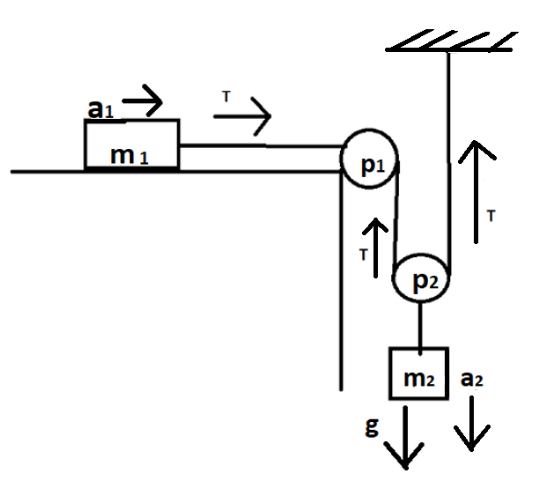
Consider two masses m1 and m2 as shown in figure. Applying tension (T) on the two masses, mass m1 is moveable because the mass of the first one is lesser than the second one hence the force applied by the second one should be larger. The acceleration on the masses is given by a1and a2 respectively. Applying tension trick,
Ta1−2Ta2=0
The tension on m2 is upward on P1 and the second tension is applied upward towards a fixed path. Hence, 2Tis applied on m2.
⇒Ta1=2Ta2
a1=2a2 ……(1)
Now applying forces on the block one, tension is pulling the box in right direction and also acceleration is applying in right hand direction T=(m1a1)=(1.5)a1 ……(2)
Force on the second block be given the acceleration is pulling the block downward due to gravity.
2g−2T=a2 ……(3)
Solving these three equations:
Putting vale of (1) in (2) , T=(1.5)2a2 ……(4)
Solving equations (3) and (4)
2g=4a2
Hence, a2=210=5ms−2
Putting in (1)
∴a1=2(5)=10ms−2
Hence the option that matches our answer is B.
Note: Tension is applied by means of string, cable, chain or a dimensional block. Tension can also be named as an action-reaction pair of forces acting at the end of block. Tension is opposite of compression. Length of the strings do not affect the tension.
