Question

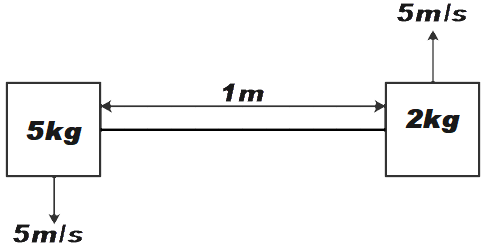
Two blocks of masses 3 Kg and 2 Kg are connected with a string of length 1 m. At any instant the velocities of blocks of masses 2 Kg and 3 Kg are 5 m/s in opposite direction and perpendicular to the length of string(Assume gravity free space)

A. tension in the string is 300 N.
B. tension in the string is 120 N.
C. tension in the string is 75 N.
D. tension in the string is 200 N.

Answer 1

To solve this particular question, we will find the velocity of centre of mass of the complete system including both blocks and string. Later, using these values we will find the centripetal force of one of these blocks with respect to centre of mass that will be equal to the tension in the string.

Formula Used:
${{v}_{cm}}=\dfrac{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
${{r}_{1}}=\dfrac{{{m}_{2}}\times r}{{{m}_{1}}+{{m}_{2}}}$
$T=\dfrac{m{{v}^{2}}}{r}$

Complete step by step answer:
We have been given,
${{m}_{1}}=2kg,{{v}_{1}}=5m/s$
${{m}_{2}}=3kg,{{v}_{2}}=-5m/s$
Now, first of all let us find the velocity of centre of mass say ${{v}_{cm}}$ of the whole system
We know,
$\Rightarrow {{v}_{cm}}=\dfrac{{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$ …………. (1)
Substituting the given values,
$\Rightarrow {{v}_{cm}}=\dfrac{\left[ \left( 2\times 5 \right)+3\left( -5 \right) \right]}{2+3}$
Therefore,
$\Rightarrow {{v}_{cm}}=-1m/s$……………… (A)
Now, let us find the velocity of block 1 with respect to the centre of mass say ${{v}_{1cm}}$
We know,
$\Rightarrow {{v}_{1cm}}={{v}_{1}}+{{v}_{cm}}$ ………… (2)
Therefore,
$\Rightarrow {{v}_{1cm}}=5-(-1)$
$\Rightarrow {{v}_{1cm}}=6m/s$…………….. (B)
Now let us find the distance between the block 1 and the centre of mass
From the formula,
$\Rightarrow {{r}_{1}}=\dfrac{{{m}_{2}}\times r}{{{m}_{1}}+{{m}_{2}}}$ ……….. (3)
$\Rightarrow {{r}_{1}}=\dfrac{3\times 1}{2+3}$
Therefore,
${{r}_{1}}=0.6m$ …………………. (C)
Now, using the formula for centripetal acceleration,
$\Rightarrow T=\dfrac{m{{v}^{2}}}{r}$
Substituting appropriate values,
We get,
$\Rightarrow T=\dfrac{mv_{1cm}^{2}}{{{r}_{1}}}$
Substituting from (B) and (C)
$\Rightarrow T=\dfrac{2\times {{6}^{2}}}{0.6}$
$\therefore T=120N$

Therefore, the correct answer is option B.

Additional Information:
Centre of mass of a system is the point where the weighted relative position of the distributed mass or system of masses has its sum equal to zero. It means that it is a unique point in space where all the mass of the system can be said to be focused relative to the position of the masses.

Note:
In this question we assumed centripetal force is equal to tension among the string. As, this system of masses is in gravity free state and the velocities of both the blocks are oriented perpendicular to the string connecting the blocks. So, in such cases the magnitude of centripetal force is equal to tension in the string.