Question: Two blocks of masses 20 kg and 50 kg are lying on a horizontal floor (coefficient of friction = 0.5)...

Question

Two blocks of masses 20 kg and 50 kg are lying on a horizontal floor (coefficient of friction = 0.5). Initially the string is stretched and blocks are at rest. Now two forces 300N and 150N are applied on two blocks as shown in figure. The acceleration of a 20kg block is 2.5K $m/{{s}^{2}}$ . Find the value of K

Answer 1

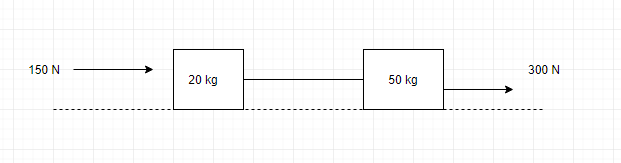
Solution

The two blocks are lying on the floor and initially at the rest. There is friction present between the blocks and the floor. So, the frictional force is there. Now both the blocks are attached by a string. So, there will be a common tension. Let it be T. when the system moves, both the blocks will have common acceleration.

Complete step by step solution:
Let the common acceleration of the system be a.
We know frictional force is always given by the product of coefficient of friction with normal reaction.
So frictional force on $50kg$ block $=\mu mg=0.5\times 50\times 10=250N$
Frictional force on $20kg$ block $=\mu mg=0.5\times 20\times 10=100N$
Both of these forces act in the backward direction while the system moves in the forward direction.
So, using Newton’s second law for this system:
$\Rightarrow 300-\left( 250+T \right)=50a \\\ \Rightarrow 300-250-T=50a \\\ \Rightarrow 50-T=50a \\\$
$\Rightarrow T=50-50a$ --(1)
For second block
$\Rightarrow 150+T-100=\text{ }20a \\\ \Rightarrow 50+T=20a \\\$
From ( $1$ ) putting the value of T we get,
$\Rightarrow 150+T-100=\text{ }20a \\\ \Rightarrow 50+50-50a=20a \\\ \Rightarrow 100=70a \\\ \Rightarrow a=\dfrac{10}{7} \\\ \therefore a=1.42m/{{s}^{2}} \\\$
But, given acceleration of $20kg$ block is $2.5K$ $m/{{s}^{2}}$
$\Rightarrow 2.5k=1.42 \\\ \Rightarrow k=\dfrac{1.42}{2.5} \\\ \therefore k=0.568 \\\$

Note: – Force is a vector and it follows the vector's law of addition. Also, here the forces acting are either in the same direction or diametrically opposite. When the forces act in the same direction we just add them. When they are opposite then we subtract them. Also, frictional force always opposed the motion. Also, if a body is at rest there will be frictional force acting on it.