Question

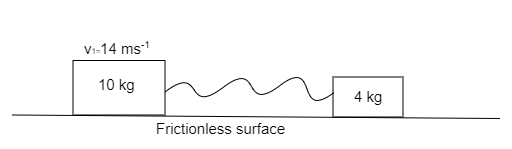
Two blocks of masses 10kg and 4kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An Impulse gives a velocity of $14\,m{s^{ - 1}}$ to the heavier block in the direction of the lighter block. What is the velocity of the center of mass?
(A) $30\,m{s^{ - 1}}$
(B) $20\,m{s^{ - 1}}$
(C) $10\,m{s^{ - 1}}$
(D) $5\,m{s^{ - 1}}$

Answer 1

The velocity of the centre of the mass can be determined by using the velocity of the centre of the mass equation. By substituting the given values in the formula directly we can determine the velocity of the centre of mass value.

Formula used:
Velocity of centre of mass,
${v_{cm}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}$
Where,
${v_{cm}}$ is the velocity of the centre of the mass, ${v_1}$ is the velocity of the first block, ${v_2}$ is the velocity of the second block, ${m_1}$ is the mass of the first block, ${m_2}$ is the mass of the second block

Complete step by step answer:
Given that,
Mass of the first block, ${m_1} = 10\,kg$
Mass of the second block, ${m_2} = 4\,kg$
Velocity of the first block, ${v_1} = 14\,m{s^{ - 1}}$
As no velocity is given to second block, assume, ${v_2} = 0\,m{s^{ - 1}}$

Velocity of centre of mass,
$\Rightarrow {v_{cm}} = \dfrac{{{m_1}{v_1} + {m_2}{v_2}}}{{{m_1} + {m_2}}}\,......................\left( 1 \right)$
By substituting the known values in the equation (1), then,
$\Rightarrow {v_{cm}} = \dfrac{{\left( {10 \times 14} \right) + \left( {4 \times 0} \right)}}{{10 + 4}}$
By simplifying the above equation, then the above equation is written as,
$\Rightarrow {v_{cm}} = \dfrac{{140 + 0}}{{14}}$
On further, the above equation is written as,
$\Rightarrow {v_{cm}} = \dfrac{{140}}{{14}}$
On dividing the above equation,
$\Rightarrow {v_{cm}} = 10\,m{s^{ - 1}}$

Then, the velocity of the centre of mass is, ${v_{cm}} = 10\,m{s^{ - 1}}$. Hence, the option (C) is the correct answer.

Note:
In this solution, the velocity of the second block is assumed to zero, because there is no velocity given to the second block. The two blocks are placed in the frictionless horizontal surface, so the second block will not get any velocity.