Question
Question: Two blocks of masses \[1\,kg\] and \[2\,kg\] rest on a smooth horizontal table.When \[2\,kg\] block ...
Two blocks of masses 1kg and 2kg rest on a smooth horizontal table.When 2kg block is pulled by a certain force F the tension T in the string is ?
A. 2FN
B. 3FN
C. 4FN
D. 5FN
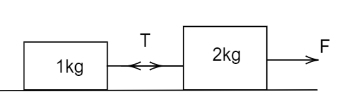
Solution
Find the equation of motion of the system from there find the acceleration of the system. Then find the tension in the string taking any of the blocks in count to calculate. Newton's law of motion states that the net force acting on a system is equal to the mass times the acceleration of the system.
Formula used:
The Newton’s second law of motion is given by,
F=ma
Where F is the force acting on the body m is the mass of the body and a is the acceleration of the body.
Complete step by step answer:
We have given here a system of two blocks which are connected by a string and a horizontal force F is applied to it. Now, first we have to find the acceleration of the system. The total mass of the system is, 1+2=3kg
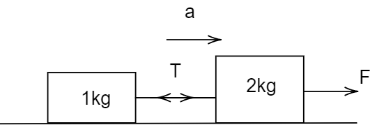
Hence, the equation of motion of the system can be written as,
F=3a
⇒a=3F
Now, to find the tension on the string we have to consider the equation of motion of any of the blocks. So, for the 2kg block the equation of motion can be written as,
F−T=2a
Putting the value of acceleration we will have,
F−T=23F
⇒F−32F=T
∴T=3F
Hence, the tension in the string will be equal to 3FN.
Hence, option B is the correct answer.
Note: We can also find the tension on the string considering the 1kg block. For that case the equation of motion of the block will become, F+T=a. Since both the tension and the force are acting in the same direction. The tension due to both the blocks must be equal to maintain the system in the same acceleration.
