Question

Two blocks of mass ${M_1} = 20kg$ and ${M_2} = 12kg$ are connected by a metal rod of mass $8kg$. The system is pulled vertically up by applying a force of $480N$ as shown. The tension at the midpoint of the rod is
(A) $144$
(B) $96$
(C) $240$
(D) $192$

Answer 1

We will first find the net acceleration of the entire system by applying Newton’s ${2^{nd}}$ Law on the whole rigid body. To find tension at the midpoint of the rod, we divide the whole system into two parts, splitting the rod, so that our first system becomes ${M_1}$ with half the rod, and the second system is the other half of the rod attached to ${M_2}$. Next we use Newton’s ${2^{nd}}$ Law to balance forces on the systems and find equations with tension at the mid-point of the rod $T$ as a variable. Using the previously calculated value of net acceleration of the system, we find the tension at the midpoint of the rod $T$.

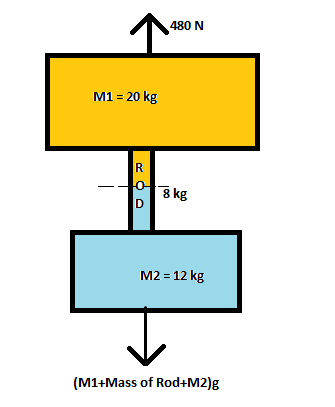
Step by step solution: We know the acceleration of the system is $a$, where it can be found by applying Newton’s ${2^{nd}}$ Law on the system,
$480N - ({M_1} + 8 + {M_2})g = ({M_1} + 8 + {M_2})a$
$\Rightarrow 480N = ({M_1} + 8 + {M_2})(a + g)$
$\Rightarrow 480 = (20 + 8 + 12)(a + 10)$
$\Rightarrow \dfrac{{480}}{{40}} = (a + 10)$
$\Rightarrow a = 2m/{s^2}$

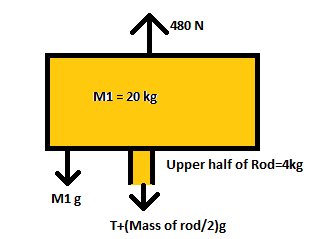
There, if the whole body is accelerating at $a = 2m/{s^2}$, then the upper half will also be accelerating at the same value of $a$
Let us assume the Tension as $T$ at the midpoint of the rod.
The net force on the first system is $480N - T - ({M_1} + 4)g = ({M_1} + 4)a$
Since the entire body is moving as a whole rigid mass with the same acceleration, here we will use the previously calculated value of $a = 2m/{s^2}$,
Therefore, since the upper half of the rod is of mass $4kg$, the equation becomes,
$\Rightarrow 480 - T - ({M_1} + 4)g = ({M_1} + 4)2$
$\Rightarrow 480 - T - (20 + 4)(10) = (20 + 4)2$
$\Rightarrow 480 - (20 + 4)12 = T$
$\Rightarrow T = 192N$

Hence option $(D)$ is correct

Note: Since the entire structure is a rigid body, the net acceleration of the system will be assumed to be uniform and the same both when the entire structure is being considered as a whole and also when the upper half of the rod and ${M_1}$ is considered.