Question

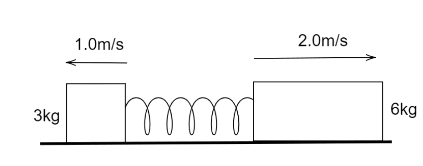
Two blocks of mass $3kg$ and $6kg$ respectively are placed on a smooth horizontal surface. They are connected by a light spring of force constant $k = 200N{m^{ - 1}}$ .Initially, the spring is unstretched. The indicated velocities are imparted to the blocks. The maximum extension of the spring will be

A. $57\,cm$
B. $25\,cm$
C. $30\,cm$
D. $15\,cm$

Answer 1

Redraw the given diagram to get a reference. Now at maximum extension, both the bodies must move with the same velocity so by covering the linear momentum we get the common velocity now using that velocity by conservation of mechanical energy we can find the maximum extension of the spring.

Complete step by step answer:
As given in the problem, there are two blocks of mass $3kg$ and $6kg$ respectively placed on a smooth horizontal surface. They are connected by a light spring of force constant $k = 200\,N{m^{ - 1}}$ .Initially, the spring is unstretched. The indicated velocities are imparted to the blocks.

We need to calculate the maximum extension of the spring.The statement maximum extension gives us information that the velocity of both the blocks will be the same.Now drawing the diagram for better understanding:

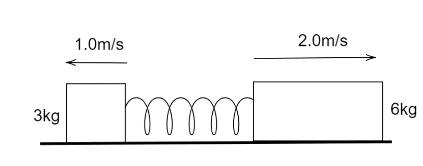
Let the common velocity of two bodies after maximum extension of the spring be $V_{com}$.Hence by conserving the linear momentum of the system we will get,
$m_1u_1 + m_2u_2 = \left( {m_1 + m_2} \right)V_{com}$
Where, Mass of the bodies equals $m_1,m_2$. Initial velocity of the two bodies is equal to $u_1,u_2$ .Final velocity of the two bodies are equal hence $V_{com}$ is the common.

Now putting the given values in the above formula of conservation of linear momentum we will get,
$m_1u_1 + m_2u_2 = \left( {m_1 + m_2} \right)V_{com}$
$\Rightarrow 3kg \times \left( { - 1.0m{s^{ - 1}}} \right) + 6kg \times \left( {2.0m{s^{ - 1}}} \right) = \left( {3kg + 6kg} \right)V_{com}$
The velocity of 3kg mass is taken as negative as it is moving the negative x-axis or we can say that it is moving opposite to that of 6kg mass body.
Further solving the above equation we will get,
$- 3m{s^{ - 1}} + 12m{s^{ - 1}} = 9V_{com}$
$\Rightarrow 9m{s^{ - 1}} = 9V_{com}$
Rearranging the above equation we will get,
$\Rightarrow Vcom = \dfrac{{9m{s^{ - 1}}}}{9}$
$\Rightarrow Vcom = 1\,m{s^{ - 1}}$

Now by using conservation of mechanical energy we will get,
Initial Energy = Final Energy
$\dfrac{1}{2}m1u{1^2} + \dfrac{1}{2}m2u{2^2} = \dfrac{1}{2}k{x^2} + \dfrac{1}{2}\left( {m1 + m2} \right)Vco{m^2}$
Where,
Spring Constant = $k$ = $200\,N{m^{ - 1}}$ (Given)
Maximum extension of the spring = $x$
$\dfrac{1}{2}3kg \times {\left( { - 1.0m{s^{ - 1}}} \right)^2} + \dfrac{1}{2}6kg \times {\left( {2.0m{s^{ - 1}}} \right)^2} = \dfrac{1}{2}200N{m^{ - 1}} \times {x^2} + \dfrac{1}{2}\left( {3kg + 6kg} \right) \times {\left( {1m{s^{ - 1}}} \right)^2}$

Cancelling all the half terms we will get,
$3\,kg \times {\left( { - 1.0m{s^{ - 1}}} \right)^2} + 6kg \times {\left( {2.0m{s^{ - 1}}} \right)^2} = 200N{m^{ - 1}} \times {x^2} + \left( {3kg + 6kg} \right) \times {\left( {1m{s^{ - 1}}} \right)^2}$
Further solving the equation we will get,
$3\,kg \times 1.0\,{m^2}{s^{ - 2}} + 6\,kg \times 4.0\,{m^2}{s^{ - 2}} = 200\,N{m^{ - 1}} \times {x^2} + \left( {3kg + 6kg} \right) \times 1\,{m^2}{s^{ - 2}}$
$\Rightarrow 3\,kg \times 1.0{m^2}{s^{ - 2}} + 6\,kg \times 4.0\,{m^2}{s^{ - 2}} = 200\,N{m^{ - 1}} \times {x^2} + 9\,kg \times 1\,{m^2}{s^{ - 2}}$
Further solving the equation we will get,
$\Rightarrow 3\,kg \times 1.0{m^2}{s^{ - 2}} + 6\,kg \times 4.0{m^2}{s^{ - 2}} = 200\,N{m^{ - 1}} \times {x^2} + 9\,kg \times 1\,{m^2}{s^{ - 2}}$
$\Rightarrow 3.0\,kg{m^2}{s^{ - 2}} + 24.0\,kg{m^2}{s^{ - 2}} = 200\,N{m^{ - 1}} \times {x^2} + 9kg{m^2}{s^{ - 2}}$

Taking common term one side we will get,
$3.0\,kg{m^2}{s^{ - 2}} + 24.0\,kg{m^2}{s^{ - 2}} - 9.0\,kg{m^2}{s^{ - 2}} = 200\,N{m^{ - 1}} \times {x^2}$
Simplifying further,
$18\,kg{m^2}{s^{ - 2}} = 200\,N{m^{ - 1}} \times {x^2}$
Rearranging the above equation we will get,
$\Rightarrow \dfrac{{18\,kg{m^2}{s^{ - 2}}}}{{200\,N{m^{ - 1}}}} = {x^2}$
$\Rightarrow \dfrac{{9\,kg{m^2}{s^{ - 2}}}}{{100\,N{m^{ - 1}}}} = {x^2}$
Further simplifying the above equation,
$0.09\,{m^2} = {x^2}$
Taking square to other sides we will get,
$0.3m = x$
Converting meter into centimeter we will get,
$\therefore x = 30\,cm$

Therefore the correct option is $\left( C \right)$.

Note: Remember whenever the spring experiences maximum extension then all the body connected with the spring will experience maximum extension.Tension is a pulling force and not a pushing force as ropes can’t push effectively. Attempting to push the rope will cause the rope to go slack, losing the tension it possesses. This might sound obvious but while illustrating the forces acting on an object, people often draw the force of tension going in the wrong direction. Hence it is important to remember that tension can only pull on an object but not push against it.