Question

Two blocks of mass $2Kg$ and $4Kg$ are accelerated with the same acceleration by a force of $10N$ as shown in figure on a smooth horizontal surface. Then the spring force between the two blocks will be (spring is massless)

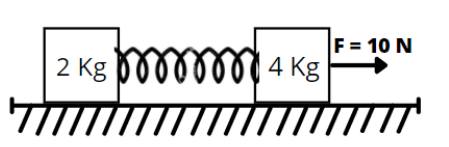
(A) $5N$
(B) $10N$
(C) $\dfrac{{10}}{3}N$
(D) $\dfrac{5}{3}N$

Answer 1

The given question can be solved with the help of a free body diagram. A free-body diagram is a diagram that represents the forces acting on a system. Here, we can find the forces acting on the entire system and each of the bodies. Here, in this system, we derive equations of equivalent forces from all other forces that act on the system.

Complete Step By Step Answer:
For finding the spring forces between the blocks, we need to represent the forces acting on the system (precisely Newton's equation of motion) systematically through a free body diagram and write equations of motion.
According to the question, two blocks of masses ${m_1} = \,2Kg$ and ${m_2}\, = \,4Kg$ are connected with a spring(a massless spring) and a force $F\, = \,10\,N$ is applied to the system.
Now, by identifying forces acting on the system, a free body diagram of the system can be drawn as

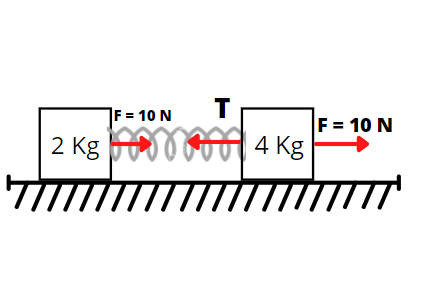
Here, we can see that a force $F\, = \,10\,N$ is applied to the system that means it is applied to both the blocks of masses ${m_1}\, = \,2\,Kg$ and ${m_2}\, = \,4\,Kg$ . Also, an opposing force(spring force, $T$ ) acts in between the blocks.
Now, as given in the question, both blocks are accelerated with the same acceleration.
So, the equation of motion of force acting on the system becomes:
$F\, = \,\,{m_1}a\, + \,{m_2}a$
Here,
Force, $F$ is applied in $N$ (Newton).
Mass of block $1$ is represented by ${m_1}\, = \,2Kg$
Mass of block $2$ is represented by ${m_2}\, = \,4\,Kg$
Acceleration, $a$ for both the blocks, is measured in ${m \mathord{\left/ {\vphantom {m {{s^2}}}} \right.} {{s^2}}}$ (meter per second square).
$F\, = \,\,{m_1}a\, + \,{m_2}a$
$\Rightarrow \,F\, = \,\left( {{m_1}\, + \,{m_2}} \right)a$
$\Rightarrow \,10\, = \,\left( {2\, + \,4} \right)\,a$
$\Rightarrow 6 = \,10$
$\Rightarrow a = \dfrac{{10}}{6}$
$\Rightarrow a = \dfrac{5}{3}$
Therefore, it can be seen that both the blocks are accelerated with the same acceleration of $a= \dfrac{5}{3}$
Now, by considering all the forces acting on the block of mass ${m_2} = 4 Kg$ ,
Since, both the blocks are accelerated with some acceleration. The force of spring acting on the block must be less than the total accelerating force of both the blocks.
$F - T= {m_2}a$
Here,
Spring force, $T$ between the blocks, is measured in $N$ (Newton).
$F - T = {m_2}a$
$\Rightarrow 10 - T = 4\ \times \dfrac{5}{3}$
Now, by subtracting $10$ from both sides of the equation, we get:
$\Rightarrow - T = \dfrac{{20}}{3}- 10$
$\Rightarrow \ - T = \dfrac{{20 - 30}}{3}$
$\Rightarrow - T = - \dfrac{{10}}{3}$
$\Rightarrow T = \dfrac{{10}}{3}$
Hence, the spring force between the two blocks is, $T = \dfrac{{10}}{3}N$
Therefore, option (C) $\dfrac{{10}}{3}N$ is the correct option.

Note:
A Free-body diagram is a significant step in the solving of motion-related problems. Since it helps to assume all the forces acting on a single object or a system. The equivalent external force acting on the object must be taken to apply Newton's Second Law to the motion to the system.