Question
Question: Two blocks of mass "2kg" & "3kg" respectively are placed on rough inclined having inclination angle ...
Two blocks of mass "2kg" & "3kg" respectively are placed on rough inclined having inclination angle θ = 37° as shown in the diagram (N is the normal reaction between the two blocks):-
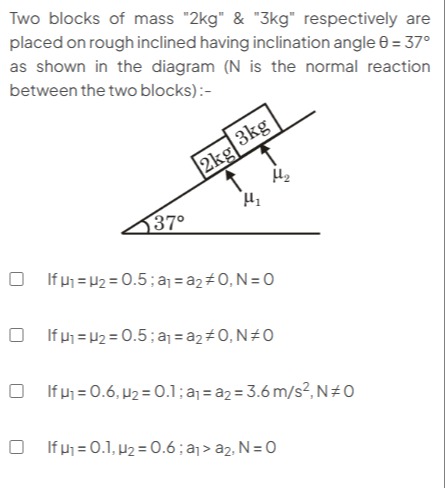
If μ₁ = μ2 = 0.5 ; a₁ = a2 ≠ 0, N = 0
If μ₁ = μ₂ = 0.5 ; a₁ = a2 ≠ 0, N≠0
If μ₁ = 0.6, μ2 = 0.1 ; a₁ = a2 = 3.6 m/s², N≠0
If μ₁ = 0.1, μ2 = 0.6 ; a₁ > a2, N = 0
If μ₁ = μ2 = 0.5 ; a₁ = a2 ≠ 0, N = 0, If μ₁ = 0.6, μ2 = 0.1 ; a₁ = a2 = 3.6 m/s², N≠0, If μ₁ = 0.1, μ2 = 0.6 ; a₁ > a2, N = 0
Solution
To analyze the motion of the two blocks, we first calculate the acceleration each block would have if it were moving independently down the incline. The acceleration of a block of mass m with coefficient of kinetic friction μ on an incline of angle θ is given by:
aind=gsinθ−μgcosθ
Given: m1=2 kg, m2=3 kg θ=37∘ We use g=10 m/s2. sin(37∘)≈0.6 cos(37∘)≈0.8
So, gsinθ=10×0.6=6 m/s2. And gcosθ=10×0.8=8 m/s2.
Thus, aind=6−8μ.
Now, let's analyze each option:
Option 1: If μ1=μ2=0.5; a1=a2=0, N=0
Calculate independent accelerations: a1ind=6−8(0.5)=6−4=2 m/s2 a2ind=6−8(0.5)=6−4=2 m/s2
Since a1ind=a2ind, both blocks tend to move with the same acceleration. Therefore, they will move together with a1=a2=2 m/s2. As there is no relative motion tendency, there will be no normal force between them, so N=0. The conditions a1=a2=0 and N=0 are met. This option is correct.
Option 2: If μ1=μ2=0.5; a1=a2=0, N=0
From the analysis of Option 1, when μ1=μ2=0.5, we found that N=0. This option states N=0, which contradicts our finding. This option is incorrect.
Option 3: If μ1=0.6,μ2=0.1; a1=a2=3.6 m/s2, N=0
Calculate independent accelerations: a1ind=6−8(0.6)=6−4.8=1.2 m/s2 a2ind=6−8(0.1)=6−0.8=5.2 m/s2
Since a2ind>a1ind, block 2 (the one behind) tends to accelerate faster than block 1 (the one in front). This means block 2 will push block 1, so they will move together with a common acceleration a, and N=0. To find the common acceleration a, treat the two blocks as a single system with total mass M=m1+m2=2+3=5 kg. The net force down the incline on the combined system is: Fnet=(m1+m2)gsinθ−(μ1m1gcosθ+μ2m2gcosθ) Fnet=(2+3)(6)−(0.6×2×8+0.1×3×8) Fnet=5×6−(9.6+2.4) Fnet=30−12=18 N The common acceleration is a=MFnet=5 kg18 N=3.6 m/s2. This matches the given acceleration a1=a2=3.6 m/s2. Since a2ind>a1ind, there must be a normal force N=0 for them to move together. (We can calculate N for verification. For m1: m1a=m1gsinθ+N−μ1m1gcosθ. 2×3.6=2×6+N−0.6×2×8 7.2=12+N−9.6 7.2=2.4+N⟹N=4.8 N, which is non-zero.) The conditions a1=a2=3.6 m/s2 and N=0 are met. This option is correct.
Option 4: If μ1=0.1,μ2=0.6; a1>a2, N=0
Calculate independent accelerations: a1ind=6−8(0.1)=6−0.8=5.2 m/s2 a2ind=6−8(0.6)=6−4.8=1.2 m/s2
Since a1ind>a2ind, block 1 (the one in front) tends to accelerate faster than block 2 (the one behind). This means block 1 will move away from block 2, and they will separate. In this case, there will be no normal force between them, so N=0. The accelerations will be their independent accelerations: a1=5.2 m/s2 and a2=1.2 m/s2. The conditions a1>a2 (5.2>1.2) and N=0 are met. This option is correct.
Therefore, options 1, 3, and 4 are correct.
