Question

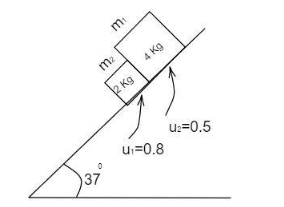
Two blocks ${m_1}$ and ${m_2}$ are resting on a rough inclined plane of inclination ${37^0}$ as shown in figure. The contact force between the blocks is, $\left( {{m_1} = 4\,Kg,\,{m_2} = 2\,Kg,\,{\mu _1} = 0.8,\,{\mu _2} = 0.5,\,g = 10\,m/{s^2},\sin {{37}^ \circ } = 3/5} \right)$

(A) $3.2\,N$
(B) $3.6\,N$
(C) $7.2\,N$
(D) Zero

Answer 1

Use the formula of the newton’s second law and from the free body diagram find the acceleration of the blocks over the inclined surface. To find the contact force between blocks, again substitute the same formula for the second block and substitute the value of the acceleration.

Useful formula:
The formula of the newton’s second law of motion is given by
$F = ma$
Where $F$ is the force, $m$ is the mass and $a$ is the acceleration.

Complete step by step solution:
It is given that the mass of the first block, ${m_1} = 4\,Kg$
Mass of the second block, ${m_2} = 2\,Kg$
The coefficient of friction of the first block, ${\mu _1} = 0.8$
The coefficient of friction of the second block, ${\mu _2} = 0.5$
The angle of the inclined surface with the horizontal, $\theta = {37^ \circ }$
Since the coefficient of friction of the first block is more than the coefficient of the fiction of the second block, then both are said to have the same acceleration. Hence

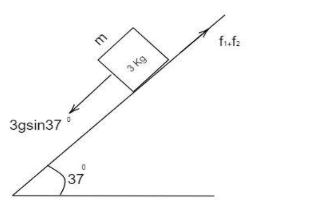
${a_1} = {a_2} = a$
So let us consider two blocks as the single block with the mass $3\,Kg$ . Separating this force into horizontal and the vertical component.
By rearranging the formula, we get
$a = \dfrac{F}{m}$
Substituting the values,
$a = \dfrac{{6g\sin {{37}^ \circ } - \left( {{f_1} + {f_2}} \right)}}{6}$
Where $f = \mu mg\cos \theta$
$a = \dfrac{{6g\sin {{37}^ \circ } - \left( {0.8 \times 2 \times 10\cos {{37}^ \circ } + 0.5 \times 4 \times 10\cos {{37}^ \circ }} \right)}}{6}$
By simplifying the above equation,
$a = \dfrac{{36 - 27.55}}{6}$
By further simplification, we get
$a = 1.41\,m{s^{ - 2}}$

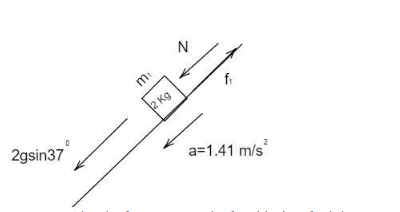
Let us consider the force acts on the first block to find the contact force between them,
By using the formula again,
$F = ma$
$2 \times 10\sin {37^0} + N - {f_1} = 2 \times a$
By simplifying,
$N = 2.84 + 12.24 - 12 = 3.2\,N$
Hence the contact force between the block is $3.2\,N$ .

Thus the option (A) is correct.

Note: Remember that the mass and the gravitational force acts in the direction of the motion of the block whereas the frictional force acts against the motion. Since the second block is located below the first block, the whole force on the first block acts on the second, hence the second block is considered to find the force of contact.