Question
Question: Two blocks, each of mass \(m = 3.50kg\) , are hung from the ceiling of an elevator as in the above f...
Two blocks, each of mass m=3.50kg , are hung from the ceiling of an elevator as in the above figure. (a) If the elevator moves with an upward acceleration a of magnitude 1.60m s−2, find the tensions T1 and T2 in the upper and lower strings. (b) If the strings can withstand a maximum tension of 85.0N, what maximum acceleration can the elevator have before a string break.
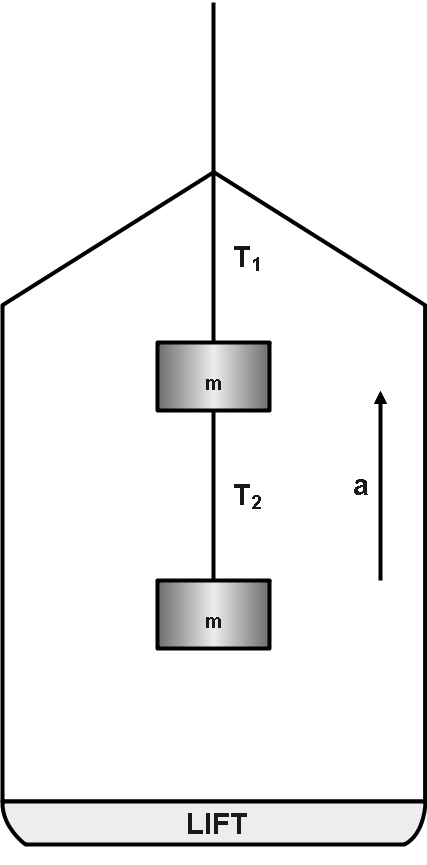
Solution
In this question there are two parts. In first part we will find the tension in both the strings and to find that we will apply NLM separately in both the blocks and simplify the net forces to get the required answer and in second part of the question we will find what maximum acceleration can the elevator have before a string break to find this we will put the value of maximum tension in the previous formula and hence we will get the required answer.
Formula used:
F=ma
Where,
F is the force,
m is the mass and
a is the acceleration.
Complete answer:
According to the question,
Mass of each block is, m=3.50kg
And, upward acceleration of the elevator, a=1.60m s−2
Here, both the blocks experience a gravitational force, and is given by,
mg=3.50×9.8 =34.3N
Now we will solve separately,
For the lower block,
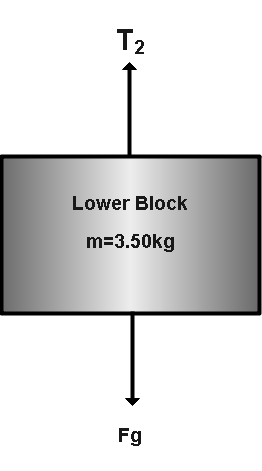
Here we will apply Newton’s 2nd law of motion.
The net force on the block is,
Now we will put the value to get the tension in the string,
T2=m(a+g) ⇒T2=3.50(1.60+9.8) ⇒T2=39.9NHence, the tension in the lower string is 39.9N .
Now, for upper block,
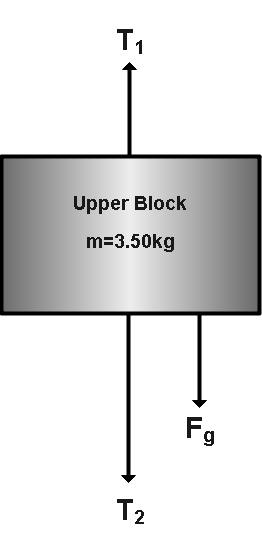
Here we will apply Newton’s 2nd law of motion.
The net force on the block is,
Now we will put the value to get the tension in the string,
T1=ma+T2+mg ⇒T1=(3.50×1.60)+39.9+(3.50×9.8) ⇒T1=5.6+39.9+34.3 ⇒T1=79.8NHence, the tension in the upper string is 79.8N .
Now, 2nd part of the answer,
We can see from the above results, the tension in the upper string is greater than the tension in the lower string, i.e., T1>T2 .
So, we can conclude that the upper string will break first when the acceleration of the system increases.
Now, we will find the maximum acceleration when T1=85.0N .
Now, the expression for the tension in the upper string is,
T1=ma+T2+mg
But, T2=ma+mg
So, the above equation becomes,
Now, rearranging the equation for a .
a=2mT1−2mg
Now, putting the values,
So, the maximum acceleration is,
a=2mT1−2mg ⇒a=2(3.5)85−2(3.5×9.8) ⇒a=785−2(34.3) ⇒a=716.4 ∴a=2.34m s−2
Hence, the maximum acceleration is 2.34m s−2 .
Note:
Newton’s laws of motion are built on the concept of Galileo’s laws of motion. Newton’s second law of motion is also known as the law of force and acceleration as an applied force on an object causes the object to accelerate. Solve the system separately for easy purposes otherwise there are chances of making mistakes and in the 2nd part of the question the maximum tension is already given. Put that in the equation instead of putting the previous value.
