Question

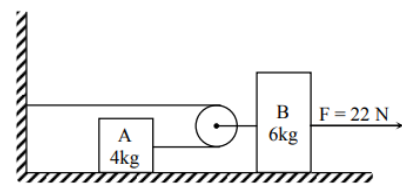
Two blocks are connected by a massless string through an ideal pulley as shown. A force of $22\,N$ is applied on block $B$ when initially the blocks are at rest. Then acceleration of centre of mass of block $A$ and block $B$, $2\,s$, after the application of force is $($ masses of $A$ and $B$ are $4\,kg$ and $6\,kg$ respectively and surfaces are smooth $)$

A. $1.4\,m{s^{ - 2}}$
B. $1\,m{s^{ - 2}}$
C. $2\,m{s^{ - 2}}$
D. None of these.

Answer 1

The point where the whole mass is assumed to be concentrated is known as the centre of mass and it is relative to an object or the system of objects and also the average position of all parts of the system, weighted according to their masses. The tension is nothing but the pulling force in the string and the direction of the string will be away from the load.

Complete step by step answer:
Given: Force exerted on the block $B$ when the blocks are at rest is $= 22\,N$
$F = 22\,N$
Mass of block $A = 4\,kg$
Mass of block $A = 6\,kg$
We need to find acceleration of centre of mass of blocks $A$ and $B$ after $2s$ from the application of force
Let the tension in the string be $T$ , then;
$F - 2T = 6a$ ……….. $\left( 1 \right)$
$\Rightarrow T = 4 \times 2a$
$\Rightarrow T = 8a$ ……….. $\left( 2 \right)$
Substituting equation $\left( 2 \right)$ in equation $\left( 1 \right)$ we get
$F - 16a = 6a$
Therefore, $a = \dfrac{F}{{22}}$
Substituting the value of $F$ in above equation we get acceleration as
$a = 1\,m{s^{ - 2}}$
Then the acceleration of the centre of mass will be
${a_{cm}} = \dfrac{{\left( {6 \times acceleration{\text{ }}of{\text{ }}A} \right) + \left( {4 \times acceleration{\text{ }}of{\text{ B}}} \right)}}{{6 + 4}}$
${a_{cm}} = \dfrac{{\left( {6 \times 1} \right) + \left( {4 \times 2} \right)}}{{10}}$
$\therefore {a_{cm}} = 1.4\,m{s^{ - 2}}$

Hence, option A is correct.

Note: By using acceleration of the centre of mass we can find speed of centre of mass that is speed of centre of mass = acceleration $\times$ time $= 1.4 \times 2 = 2.8m{s^{ - 1}}$ because the acceleration is defined as rate of change of velocity. Is is a vector quantity and its $S.I$ unit is $m{s^{ - 2}}$.