Question
Question: Two blocks \(A\) and \(B\) of same mass \(m\) attached with a light spring are suspended by a string...
Two blocks A and B of same mass m attached with a light spring are suspended by a string as shown in figure. Find the acceleration of block A and B just after the string is cut.
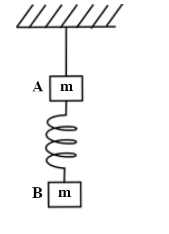
Solution
In this question, we make use of the concept of free body diagram and write the equations for force in each given case. Then, we find the acceleration of both blocks using force equations on both the blocks using free body diagrams and substituting the value of given data into the equations.
Complete step by step answer:
Consider the case when the string is not cut. k be the spring constant and x be the displacement caused by spring. Then, restoring force F=−kx
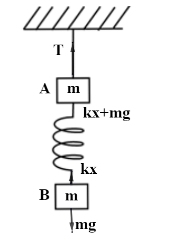
Now, for block A, we have from free body diagram,
mg−kx=0
∴mg=kx−−−−−−−−−−−−(1)
For block B, we have
kx+mg−T=0
From (1) , we get
∴2mg=T−−−−−−−−(2)
Where, T - tension in the string
Now, consider the case when the string is cut, tension in the string T will become zero, but the restoring force due to spring will be the same.
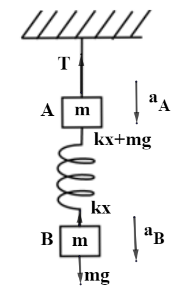
Thus, After the string is just cut, the equations for block A & B are changed.
aA - acceleration of block A
aB - acceleration of block B
For block A , mg−kx=maB
Using eq (1) ,
∴aB=0
And for block B, mg+kx=maA
⇒mg+mg=maA
∴aA=2g
Hence, acceleration of block A is 2g and acceleration of block B is 0.
Note: The free body diagram of both the cases should be correct. Do not forget the negative sign in the expression of restoring force. It will generate false results. If the spring has mass M and a mass m is suspended from it, then the total effective mass is given as Meff=m+3M.
