Question

Two blocks A and B of masses 3m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. What are the magnitudes of acceleration of A and B immediately after the string is cut respectively?

A) $g,g$
B) $g,\dfrac{g}{3}$
C) $\dfrac{g}{3},g$
D) $\dfrac{g}{3},\dfrac{g}{3}$

Answer 1

Hint : In this solution, we will make the free body diagram of the blocks before and after the string is cut. The tension in the string on block A will be different before and after the string is cut.

Complete step by step answer
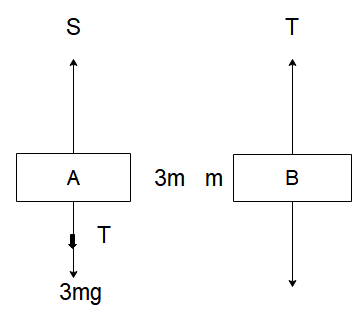
We’ve been given that two blocks A and B of masses 3m and m respectively are connected by a massless and inextensible string. Let $T$ be the tension in the string and $S$ be the spring force exerted on block A. Then the free body diagram of the blocks before the string is cut will be

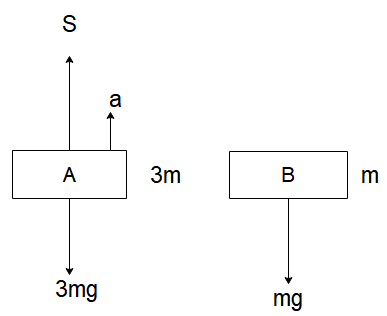
And the free body diagram of the system after the string is cut will be

When the string is not cut, the system will be in equilibrium with the spring being expanded due to the weight of the blocks. For block A, we can write
$\Rightarrow S = T + 3mg$
And for block B
$\Rightarrow T = mg$ . Substituting this relation in equation (1), we get
$\Rightarrow S = 4mg$
Now that we know the spring force, let us tackle the situation when the string is cut. When the string is cut, both the blocks will have some acceleration. For block B, since it is accelerating only under the influence of gravity and no other external force, it will have acceleration $g$ . For block A, we can say from the free body diagram that
$\Rightarrow S - 3mg = 3ma$
Since $S = 4mg$ , we can say
$\Rightarrow mg = 3ma$
$\therefore a = \dfrac{g}{3}$
Hence the block A will have acceleration $g/3$ and block B will have acceleration $g$ .
So option C is the correct choice.

Note
The blocks will only have acceleration when the string is cut and not before that since equilibrium will have been established. However, we must also draw the free body diagram before the string is cut to calculate the spring force acting on the system since it will influence the acceleration of block A after the string is cut.