Question

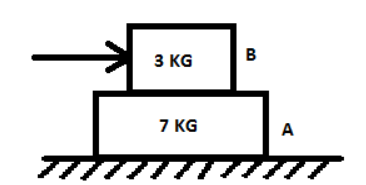
Two blocks A and B are placed one over the other on a smooth horizontal surface. The maximum horizontal force that can be applied on the upper block B, so that A and B move without separation is 49N. The coefficient of friction between A and B is:

A. 0.2
B. 0.3
C. 0.5
D. 0.8

Answer 1

Hint: As there are two blocks one over the other, we use the equation of motion of two block-systems. That is ${{\text{F}}_{{\text{max}}}} = \mu \left( {{{\text{M}}_{\text{A}}} + {{\text{M}}_{\text{B}}}} \right).{\text{g}}$. From this equation we can derive the coefficient of friction that is $\mu = \dfrac{{{{\text{F}}_{{\text{max}}}}}}{{\left( {{{\text{M}}_{\text{A}}} + {{\text{M}}_{\text{B}}}} \right).{\text{g}}}}$. Where ${{\text{M}}_{\text{A}}}$ and ${{\text{M}}_{\text{B}}}$ are the masses of the blocks.

Complete step-by-step answer:
Given, two blocks A and B are placed one over the other on a smooth horizontal surface.
The maximum horizontal force that can be applied on the upper block B, so that A and B move without separation is, ${{\text{F}}_{{\text{max}}}} = 49{\text{N}}$
Mass of Block A, ${{\text{M}}_{\text{A}}} = 7{\text{ Kg}}$
Mass of Block B, ${{\text{M}}_{\text{B}}} = 3{\text{ Kg}}$
Then coefficient of friction between A and B,$\mu = ?$
Coefficient of friction ($\mu$): Coefficient of friction is defined as the ratio of the force required to move two sliding surfaces over each other, and the force holding them together. Coefficients of friction range from near zero to greater than one.
Force: A force is a push or pull upon an object resulting from the object's interaction with another object.
Newton’s second law, F= ma
Where F is force, m is mass of an object and ‘a’ is acceleration.
Equation of motion of two blocks-systems:
${{\text{F}}_{{\text{max}}}} = \mu \left( {{{\text{M}}_{\text{A}}} + {{\text{M}}_{\text{B}}}} \right).{\text{g}}$
$\Rightarrow \mu = \dfrac{{{{\text{F}}_{{\text{max}}}}}}{{\left( {{{\text{M}}_{\text{A}}} + {{\text{M}}_{\text{B}}}} \right).{\text{g}}}}$
Where ${{\text{M}}_{\text{A}}}$ and ${{\text{M}}_{\text{B}}}$ are the masses of the blocks.
$\Rightarrow \dfrac{{49}}{{\left( {7 + 3} \right) \times 9.8}}$
$\Rightarrow \dfrac{{49}}{{\left( {10} \right) \times 9.8}}$
$\Rightarrow \dfrac{{49}}{{98}} = \dfrac{1}{2}$
$= 0.5$
Therefore, Coefficient of friction between two blocks A and B, $\mu = 0.5$

Note: The coefficient of friction is a constant ratio and is symbolized by the Greek letter mu ($\mu$). Mathematically, $\mu = {\text{F/L}}$. As both load and friction are measured in units of force, the coefficient of friction is dimensionless. And also the coefficient of friction depends on the objects that are causing friction.