Question

Two blocks (A) 2kg and (B) 5kg rest one over the other on a smooth horizontal plane. The coefficient of static and dynamic friction between (A) and (B) is the same and equal to 0.60. The maximum horizontal force that can be applied to (B) in order that both (A) and (B) do not have any relative motion:
A. 42 N
B. 42 kgf
C. 5.4 kgf
D. 1.2 N

Answer 1

Since there is no relative motion between the two blocks, the acceleration of the both blocks must be the same. For the block A to not move relative to the block B, the applied force on the block A must be equal to the frictional force between the blocks. Determine the force on the block B in units of newton.

Formula used:
Frictional force, ${f_r} = \mu N = \mu mg$,
where, $\mu$ is the coefficient of friction, N is the normal force, m is the mass and g is the acceleration due to gravity.

Complete step by step answer:
We have given that there is no relative motion between the two blocks. Therefore, the acceleration of the both blocks must be the same.

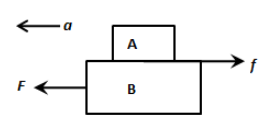
Using Newton’s second law, we can express the applied force on the system of the blocks as,
$F = \left( {{m_A} + {m_B}} \right)a$
$\Rightarrow a = \dfrac{F}{{{m_A} + {m_B}}}$
Here, ${m_A}$ is the mass of the block A, ${m_B}$ is the mass of the block B and a is the acceleration of the two blocks.
Substitute 2 kg for ${m_A}$ and 5 kg for ${m_B}$ in the above equation, we get,
$a = \dfrac{F}{{2 + 5}}$
$\Rightarrow a = \dfrac{F}{7}$ …… (1)

For the block A to not move relative to the block B, the applied force on the block A must be equal to the frictional force between the blocks. Therefore, we can write,
${F_A} = f$
$\Rightarrow {m_A}a = \mu {m_A}g$
$\Rightarrow a = \mu g$
Here, $\mu$ is the coefficient of the friction and g is the acceleration due to gravity.
Using equation (1) in the above equation, we get,
$\dfrac{F}{7} = \mu g$
$\Rightarrow F = 7\mu g$
Substituting $\mu = 0.6$ and $g = 10\,{\text{m/}}{{\text{s}}^2}$ in the above equation, we get,
$F = 7\left( {0.6} \right)\left( {10} \right)$
$\therefore F = 42\,{\text{N}}$
Therefore, the maximum horizontal force applied to block B is 42 N.

So, the correct answer is option A.

Note: The value of coefficient of friction always lies between 0 and 1. The coefficient of friction is a unit less quantity. The unit of force is sometimes expressed as kgf. It is weight equivalent force and has the value equal to 9.8 N. Therefore, the option B cannot be true.