Question

Two billiard balls of the same size and mass are in contact on a billiard table. A third ball of same size and mass strikes them symmetrically and remains at rest after the impact. Coefficient of restitution between the balls is-
(A) $\dfrac{1}{2}$
(B) $\dfrac{2}{3}$
(C) $\dfrac{2}{5}$
(D) $\dfrac{3}{4}$

Answer 1

Hint Coefficient of restitution is defined as the ratio of final relative velocity to the initial relative velocity between two objects. When the third ball strikes them symmetrically, it does so by making an angle of $30^\circ$from the normal line between the balls.

Complete Step by step solution
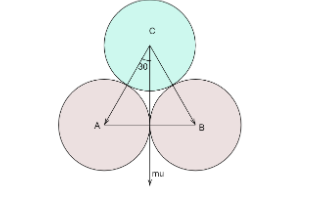
It is given that the two billiard balls are in contact, which means that the balls are either in rest or move with same velocity, let them be balls A and B.

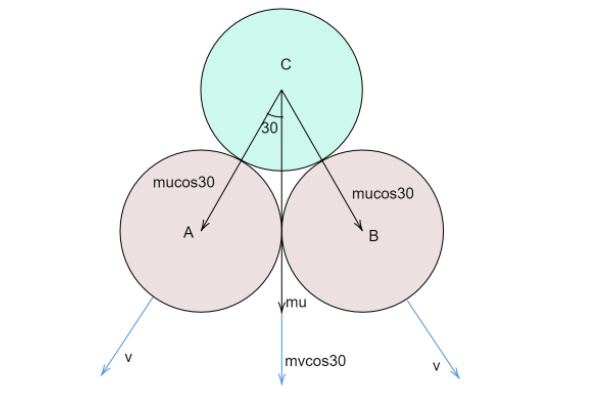
Let the initial velocity of the third ball C be, $u$
Then the initial momentum of the ball C is given as,
$p = mu$
There is no external force acting in the system, the net change in momentum is zero, which means the total momentum is constant.
Let the final velocity of ball A (or B) be, $v$
Then, as per conservation of linear momentum along the vertical line we have-
${m_A}{u_A} + {m_B}{u_B} + {m_C}{u_C} = {m_A}{v_A} + {m_B}{v_B} + {m_C}{v_C}$
The mass of all balls is same,
The initial velocity of balls A and B is taken zero,
And final velocity of ball C is taken zero.
The ball C approaches the other balls at an angle of $30^\circ$from the vertical.
Therefore, velocity of approach$= u\cos 30^\circ$
Along the vertical line, the momentum equation can be reduced to,
$mu + 0 + 0 = 0 + mv\cos \theta + mv\cos \theta$
$mu = 2mv\cos \theta$
From here,
$v = \dfrac{u}{{2\cos \theta }}$
$v = \dfrac{u}{{{{2 \times \sqrt 3/2 }}}} = \dfrac{u}{{\sqrt 3 }}$
After the collision, each ball starts moving along their line of impact with the velocity of separation and this velocity is equal to $v$.
The coefficient of restitution(e) is given by-
$e = \dfrac{{{v_{sep}}}}{{{v_{app}}}}$
Where${v_{sep}}$ is the velocity of separation and ${v_{app}}$ is the velocity of approach.
On putting the values,
$e = \dfrac{v}{{u\cos 30^\circ }}$
$e = \dfrac{{u/\sqrt 3 }}{{\dfrac{{u \times \sqrt 3 }}{2}}}$
$e = \dfrac{2}{{\sqrt 3 \times \sqrt 3 }} = \dfrac{2}{3}$
The coefficient of restitution is $\dfrac{2}{3}$.

Hence, the correct option is (B).

Note The angle $\theta$ is found using the shape of formation created by the three balls. Since they are of the same size, when the ball C hits symmetrically, the centers of all three balls form an equilateral triangle. The vertical line, along which the initial velocity of Ball C is, bisects one of the vertices of the triangle, thus this angle is equal to $30^\circ$.