Question

Two billiard balls are rolling on a flat table. One has velocity components ${{V}_{x}}=1m{{s}^{-1}},{{V}_{y}}=\sqrt{3}m{{s}^{-1}}$ and the other has components ${{V}_{x}}=2m{{s}^{-1}},{{V}_{y}}=2m{{s}^{-1}}$. If both the balls start moving from the same point, the angle between their path is:
A.${{60}^{\circ }}$
B.${{45}^{\circ }}$
C.${{22.5}^{\circ }}$
D.${{15}^{\circ }}$

Answer 1

Two components of velocity, namely, x-component and y-component, are given in the problem. This implies that the balls are performing motion in the XY-plane. We shall find the relative velocity of one billiard ball with respect to the other. Further, we will use the basic knowledge of vectors to find the angle of this relative velocity and then use properties of trigonometry to find the actual angle.

Complete answer:

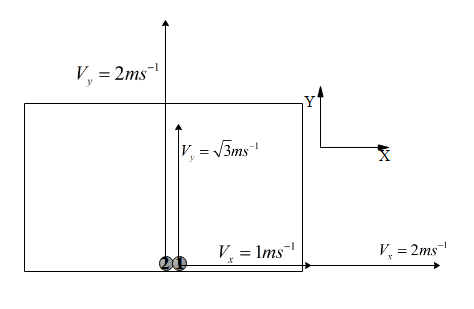
The relative velocity, ${{V}_{12}}$ of the two balls 1 and 2 is expressed as,
${{V}_{12}}={{V}_{2}}-{{V}_{1}}$
Where,
${{V}_{1}}=$ velocity of billiard ball 1
${{V}_{2}}=$ velocity of billiard ball 2
Applying the formula of relative velocity to the x-components of velocity, our equation modifies as ${{V}_{{{12}_{x}}}}={{V}_{{{2}_{x}}}}-{{V}_{{{1}_{x}}}}$.
Here, we have ${{V}_{{{1}_{x}}}}=1m{{s}^{-1}}$ and ${{V}_{{{2}_{x}}}}=2m{{s}^{-1}}$.
$\Rightarrow {{V}_{{{12}_{x}}}}=2-1$
$\Rightarrow {{V}_{{{12}_{x}}}}=1m{{s}^{-1}}$
Therefore, the x-component of relative velocity is $1m{{s}^{-1}}$.
Similarly, applying the formula of relative velocity to the x-components of velocity, our equation modifies as ${{V}_{{{12}_{y}}}}={{V}_{{{2}_{y}}}}-{{V}_{{{1}_{y}}}}$.
Here, we have ${{V}_{{{1}_{y}}}}=\sqrt{3}m{{s}^{-1}}$ and ${{V}_{{{2}_{x}}}}=2m{{s}^{-1}}$.
$\Rightarrow {{V}_{{{12}_{y}}}}=2-\sqrt{3}$
$\Rightarrow {{V}_{{{12}_{y}}}}=\left( 2-\sqrt{3} \right)m{{s}^{-1}}$
Therefore, the y-component of relative velocity is $\left( 2-\sqrt{3} \right)m{{s}^{-1}}$.
In order to find the angle, we use the property $\tan \theta =\dfrac{{{V}_{y}}}{{{V}_{x}}}$.
Here, we have ${{V}_{y}}={{V}_{{{12}_{y}}}}=\left( 2-\sqrt{3} \right)m{{s}^{-1}}$ and ${{V}_{x}}={{V}_{{{12}_{x}}}}=1m{{s}^{-1}}$. Thus, the angle, $\theta$ between their path is given as:
$\Rightarrow \tan \theta =\dfrac{2-\sqrt{3}}{1}$
We shall use the formula of $\tan 2\theta =\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$ and substitute the respective values.
$\Rightarrow \tan 2\theta =\dfrac{2\left( 2-\sqrt{3} \right)}{1-{{\left( 2-\sqrt{3} \right)}^{2}}}$
Opening the brackets in the denominator and writing the square of $2-\sqrt{3}$, we get

& \Rightarrow \tan 2\theta =\dfrac{2\left( 2-\sqrt{3} \right)}{1-\left( 4+3-4\sqrt{3} \right)} \\\ & \Rightarrow \tan 2\theta =\dfrac{2\left( 2-\sqrt{3} \right)}{1-7+4\sqrt{3}} \\\ & \Rightarrow \tan 2\theta =\dfrac{2\left( 2-\sqrt{3} \right)}{4\sqrt{3}-6} \\\ \end{aligned}$$ Taking $2\sqrt{3}$ common in the denominator, we get $$\Rightarrow \tan 2\theta =\dfrac{2\left( 2-\sqrt{3} \right)}{2\sqrt{3}\left( 2-\sqrt{3} \right)}$$ Now, cancelling $\left( 2-\sqrt{3} \right)$ and 2 from numerator and denominator, we get $$\Rightarrow \tan 2\theta =\dfrac{1}{\sqrt{3}}$$ But $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$, therefore, $$\Rightarrow \tan 2\theta =\tan {{30}^{\circ }}$$ This implies that $2\theta ={{30}^{\circ }}$. $\therefore \theta ={{15}^{\circ }}$ Therefore, the angle between their path is ${{15}^{\circ }}$. **Therefore, the correct answer is (D) ${{15}^{\circ }}$.** **Note:** Another method of solving this problem was by first finding the dot product of the two vectors of velocity of the billiard balls and then using that dot product to find the angle between them. For this method, we must have prior knowledge of finding the magnitude and dot product of vectors.