Question

Two beams, A and B, of plane polarized light with mutually perpendicular planes of polarization are seen through a Polaroid. From the position when the beam A has maximum intensity (and beam B has zero intensity), a rotation of Polaroid through ${30^ \circ }$ makes the two beams appear equally bright. If the initial intensities of the two beams are ${{{I}}_{{A}}}$ and ${{{I}}_{{B}}}$ respectively, then ${{{I}}_{{A}}}/{{{I}}_{{B}}}$ equals:
(A) $1$
(B) $1/3$
(C) $3$
(D) $3/2$

Answer 1

Hint : To solve this question, we need to find out the initial position of the Polaroid with respect to the beams A and B. Then after the given rotation, we have to find its final position with respect to the both beams. Finally using the Malus law we can get the final answer.

Formula used: The formula used to solve this question is given by
$I = {I_0}{\cos ^2}{{\theta }}$ , here $I$ is the intensity of light transmitted through a Polaroid whose axis is inclined at an angle of ${{\theta }}$ , and ${I_0}$ is the original intensity.

Complete step by step answer
We know that a Polaroid allows the components of the vibration of a light which are parallel to its axis. All the vibration components perpendicular to the axis of the Polaroid are restricted by the Polaroid. The intensity of the transmitted light as seen from the Polaroid is given by the Malus law as
$I = {I_0}{\cos ^2}{{\theta }}$ ………..(1)
From the above relation, we can see that the intensity of the transmitted light from the Polaroid is maximum when ${{\theta }} = {0^ \circ }$ , and it is minimum for ${{\theta }} = {90^ \circ }$ .
According to the question the initial position of the Polaroid is such that the beam A has maximum intensity, while the beam B has minimum intensity. So vibrations of the beam A must be parallel, and that of the beam B must be perpendicular to the Polaroid axis, as shown in the below diagram.

Now, according to the question, the Polaroid is rotated through an angle of ${30^ \circ }$ , as shown below.

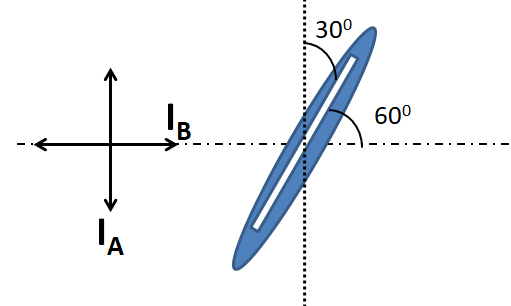
As we can see that now the Polaroid axis is inclined at an angle of ${30^ \circ }$ with the direction of the beam A, and at an angle of ${60^ \circ }$ with the direction of the beam B.
For beam A:
According to the question, the initial intensity of beam A is ${{{I}}_{{A}}}$ . Also, the angle between the Polaroid axis and the beam A is equal to ${30^ \circ }$ . Therefore substituting ${I_0} = {{{I}}_{{A}}}$ and ${{\theta }} = {30^ \circ }$ in (1) we get
${I_{{A}}}' = {I_{{A}}}{\cos ^2}{30^ \circ }$ ………..(2)
For beam B:
According to the question, the initial intensity of beam B is ${{{I}}_{{B}}}$ . Also, the angle between the Polaroid axis and the beam A is equal to ${60^ \circ }$ . Therefore substituting ${I_0} = {{{I}}_{{B}}}$ and ${{\theta }} = {60^ \circ }$ in (1) we get
${I_{{B}}}' = {I_{{B}}}{\cos ^2}{60^ \circ }$ ………..(3)
According to the question, the two beams are appearing equally bright as seen from the Polaroid. This means that the intensities of the transmitted light of the beams A and B are equal, that is,
${I_{{A}}}' = {I_{{B}}}'$
From (2) and (3)
${I_{{A}}}{\cos ^2}{30^ \circ } = {I_{{B}}}{\cos ^2}{60^ \circ }$
$\Rightarrow \dfrac{{{I_{{A}}}}}{{{I_{{B}}}}} = \dfrac{{{{\cos }^2}{{60}^ \circ }}}{{{{\cos }^2}{{30}^ \circ }}}$
We know that $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$ and $\cos {60^ \circ } = \dfrac{1}{2}$ . Therefore we get
$\dfrac{{{I_{{A}}}}}{{{I_{{B}}}}} = \dfrac{{{{\left( {1/2} \right)}^2}}}{{{{\left( {\sqrt 3 /2} \right)}^2}}}$
$\Rightarrow \dfrac{{{I_{{A}}}}}{{{I_{{B}}}}} = \dfrac{1}{3}$
Thus, the required ratio is equal to $1/3$ .
Hence, the correct answer is option B.

Note
We should always try to draw the diagram corresponding to this type of problem. This is done in order to be sure about the angle of inclination of the Polaroid axis with respect to the light beam.