Question

Two batteries of emf $18V$ and internal resistance $2\Omega$ and the other of emf $12V$ and internal resistance $1\Omega$ are connected as shown. Voltmeter V will record the reading of:

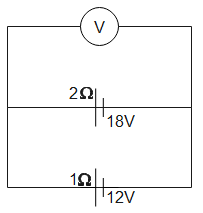
(A).$18V$
(B). $30V$
(C). $14V$
(D). $15V$

Answer 1

The figure shows two batteries and a voltmeter connected in parallel. A voltmeter is a device which is used to calculate the potential drop between two points. As the batteries are connected in parallel, they are in parallel combination. We can substitute values of voltage and internal resistance in the formula for equivalent potential in parallel combination of batteries and the equivalent potential is equal to the reading in voltmeter.
Formulas used:
$V=\dfrac{{{E}_{1}}{{r}_{2}}+{{E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}$

Complete answer:
According to the Ohm’s law,
$R=\dfrac{V}{I}$
Here, $R$ is the resistance
$V$ is the potential in the circuit
$I$ is the current in the circuit

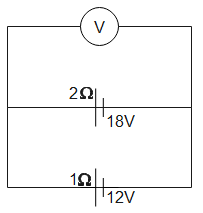
In the figure given, the two batteries and the voltmeter are connected in parallel, therefore, the potential drop in each arm will be the same. Since the batteries are connected in a parallel combination, the voltage of the resultant battery can be calculated as
$V=\dfrac{{{E}_{1}}{{r}_{2}}+{{E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}$
Here, ${{E}_{1}}$ and ${{E}_{2}}$ are the potentials of the batteries
${{r}_{1}}$ and ${{r}_{2}}$ are their internal resistances
Given, ${{E}_{1}}=18V,\,{{r}_{1}}=2\Omega$ and ${{E}_{2}}=12V,\,{{r}_{2}}=1\Omega$
Substituting given values in the above equation, we get,
$\begin{aligned} & V=\dfrac{18\times 1+12\times 2}{2+1} \\\ & \Rightarrow V=14V \\\ \end{aligned}$

The resultant circuit will be as above the potential of resultant battery will be $14V$. Since the voltmeter is connected in parallel with the battery, its potential will be the same as that of the battery.
Therefore, the reading of voltmeter will be $14V$.

Hence, the correct option is (C).

Note:
The batteries can be connected in two combinations; series and parallel and the equivalent battery is the combination of all batteries. In series, the current is the same while in parallel, the voltage is the same that is why the ammeter is connected in series while the voltmeter is connected in parallel.