Question
Question: Two batteries of e.m.f 4V and 8V with internal resistances \(1\Omega \) and \(2\Omega \) are connect...
Two batteries of e.m.f 4V and 8V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q are:-
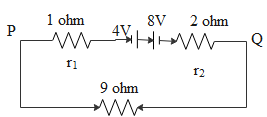
(1)31A&3V(2)61A&4V(3)91A&9V(4)21A&12V
Solution
First calculate the net potential in the circuit. Then calculate the net resistance in the circuit. Here the three resistances are connected in series. Hence use the equation of series to calculate the resistance. That will be the sum of those three resistances. Then calculate the current using net voltage and net resistance. Thus the voltage between P and Q will be the product of current and resistance.
Formula used:
Ohm’s law, V=IR
where, V is the voltage
I is the current
R is the resistance
Complete answer:
There are two batteries in the circuit. They are connected in reverse polarities.
Hence, the net potential is,
Vnet= 8V-4V=4V
Given that,
R=9Ωr1=1Ωr2=2Ω
Here the three resistance are connected in series,
Rnet=R+r1+r2
⇒Rnet=9Ω+1Ω+2Ω
⇒Rnet=12Ω
By substituting the values of net voltage and resistance the current in the circuit is,
I=RnetVnet
⇒I=124=31A
Across P and Q the potential difference is,
V=IR
Thus by substituting the values we get,
⇒V=31×9
⇒V=3V
So, the correct answer is “Option A”.
Note:
According to Ohm’s law the potential difference between two points is directly proportional to the current and the constant of proportionality is called the resistance.While calculating the net potential, always consider the polarities of the batteries in the circuit. The net resistance in case of series arrangement is their algebraic sum, whereas if the resistances are connected in parallel, the reciprocal of net resistance is the algebraic sum of reciprocals of each resistance.
